题目内容
两灯塔A,B与海洋观察站C的距离都等于20km,灯塔A在C北偏东30°,B在C南偏东60°,则A,B之间相距( )km.
| A、20 | ||
| B、30 | ||
| C、40 | ||
D、20
|
考点:余弦定理的应用
专题:计算题,解三角形
分析:由题意,∠ACB=120°,AC=20km,BC=20km,利用余弦定理,可得结论.
解答:
解:由题意,∠ACB=120°,AC=20km,BC=20km,
∴由余弦定理,可得AB2=AC2+BC2-2AC•BC•cos∠ACB=1200,
∴AB=20
km
故选:D.
∴由余弦定理,可得AB2=AC2+BC2-2AC•BC•cos∠ACB=1200,
∴AB=20
| 3 |
故选:D.
点评:本题考查余弦定理的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=2x+y的最大值与最小值之差为( )
|
| A、2 | B、3 | C、4 | D、6 |
如图给出了计算3+5+7+…+19的值的一个程序框图,其中空白处应填入( )


| A、i>9 | B、i>10 |
| C、i>19 | D、i>20 |
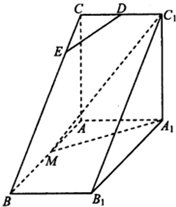 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点. 若f(x)=sin(
若f(x)=sin(