题目内容
1.已知函数$f(x)=\left\{\begin{array}{l}|{lnx}|\\ 2-lnx\end{array}\right.$$\begin{array}{l}0<x≤e\\ x>e\end{array}$,若正实数a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围为( )| A. | (e,2e+e2) | B. | $(\frac{1}{e}+2e,2+{e^2})$ | C. | $(\frac{1}{e}+e,2+{e^2})$ | D. | $(\frac{1}{e}+e,2e+{e^2})$ |
分析 图解法,画出函数$f(x)=\left\{\begin{array}{l}|{lnx}|\\ 2-lnx\end{array}\right.$$\begin{array}{l}0<x≤e\\ x>e\end{array}$的图象,根据图象分析可得a+b+c的取值范围.
解答 解:如图,画出函数$f(x)=\left\{\begin{array}{l}|{lnx}|\\ 2-lnx\end{array}\right.$$\begin{array}{l}0<x≤e\\ x>e\end{array}$的图象,
设a<b<c,则|lna|=|lnb|,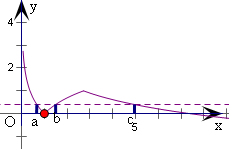
即有lna+lnb=0,即有ab=1,
当x>e时,y=2-lnx递减,
且与x轴交于(e2,0),
∴e<c<e2,
可得$\frac{1}{e}$<a<1,
当a趋近于$\frac{1}{e}$时,b,c趋近于e;
当a趋近于1时,b趋近于e,c趋近于e2,
可得a+b+c的取值范围是($\frac{1}{e}$+2e,2+e2).
故选:B.
点评 此题是个中档题.考查利用函数图象分析解决问题的能力,以及对数函数图象的特点,体现数形结合的思想.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
12.若复数z满足|z|•$\overline{z}$=20-15i,则z为( )
| A. | 4+3i | B. | 4-3i | C. | 3+4i | D. | 3-4i |
9.用数学归纳法证明不等式$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{{{2^n}-1}}<n(n∈{N^*},n≥2)$,在验证n=n0(n0为起始值)时,不等式左边为( )
| A. | 1 | B. | $1+\frac{1}{2}$ | ||
| C. | $1+\frac{1}{2}+\frac{1}{3}$ | D. | $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{{{2^{n_0}}-1}}$ |
6.下列函数中,是偶函数且在区间(0,1)上单调递增为的是( )
| A. | y=ln(x+1) | B. | y=$\frac{1}{2}$x2+cosx | C. | y=x4-3x2 | D. | y=3x+sinx |
 如图所示,在著名的汉诺塔问题中有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n),则f(6)=( )
如图所示,在著名的汉诺塔问题中有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n),则f(6)=( )