题目内容
已知x1+x13=3,x2+
=3,求x1+x2的值.
| 3 | x2 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:根据方程和函数之间的关系,结合反函数的性质即可得到结论.
解答:
 解:由x1+x13=3得x13=3-x1,
解:由x1+x13=3得x13=3-x1,
由x2+
=3得
=3-x2,
∵函数y=x3和y=
互为反函数,∴它们的图象关于y=x对称,
作出y=3-x的图象,
则A(x1,y1),B(x2,y2)关于C对称,
由
,解得
,
则
=
,
即x1+x2=3.
 解:由x1+x13=3得x13=3-x1,
解:由x1+x13=3得x13=3-x1,由x2+
| 3 | x2 |
| 3 | x2 |
∵函数y=x3和y=
| 3 | x |
作出y=3-x的图象,
则A(x1,y1),B(x2,y2)关于C对称,
由
|
|
则
| x1+x2 |
| 2 |
| 3 |
| 2 |
即x1+x2=3.
点评:本题主要考查方程根的应用,例反函数的性质是解决本题的关键.

练习册系列答案
相关题目
已知sinα=-
,且α是第四象限角,则tanα的值为( )
| 3 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知点P在定圆O的圆内或圆周上,动圆C过点P与定圆O相切,则动圆C的圆心轨迹可能是( )
| A、圆或椭圆成双曲线 |
| B、两条射线或圆或抛物线 |
| C、两条射线或圆或椭圆 |
| D、椭圆或双曲线或抛物线 |
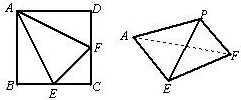 正方形ABCD的边长为1,E、F分别为BC、CD的中点,沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P,则P到面AEF的距离为
正方形ABCD的边长为1,E、F分别为BC、CD的中点,沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P,则P到面AEF的距离为