题目内容
在直角坐标系xoy中,点P到两点F1(-
,0),F2(
,0)的距离之和等于4,设P点的轨迹为曲线C,过点M(1,0)的直线l与曲线C交于A、B两点.
(1)求曲线C的方程;
(2)若抛物线:y2=2px(p>0)与曲线C交于不同两点P、Q,且
=
,求抛物线的通径;
(3)求
•
的取值范围.
| 3 |
| 3 |
(1)求曲线C的方程;
(2)若抛物线:y2=2px(p>0)与曲线C交于不同两点P、Q,且
| PF2 |
| F2Q |
(3)求
| OA |
| OB |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(1)易知曲线C为椭圆,由定义可知c=
,a=2,从而有b2=1;
(2)由
=
且椭圆和抛物线都关于x轴对称,知PQ⊥x轴,可得xP=xQ=
,代入椭圆的方程可求点P、Q坐标,代入抛物线方程可求p值;
(3)分情况讨论:斜率为0及斜率不存在时易求
•
的值;斜率存在且不为0时,设l:x=my+1,A(x1,y1),B(x2,y2),联立
,得(m2+4)y2+2my-3=0,利用韦达定理及向量数量积运算可表示
•
为m的表达式,利用函数性质可求范围;
| 3 |
(2)由
| PF2 |
| F2Q |
| 3 |
(3)分情况讨论:斜率为0及斜率不存在时易求
| OA |
| OB |
|
| OA |
| OB |
解答:
解:(1)由题意知曲线C为以F1(-
,0),F2(
,0)为焦点的椭圆,
且c=
,a=2,∴b2=1,
∴曲线C的方程为:
+y2=1;
(2)∵
=
且椭圆和抛物线都关于x轴对称,∴PQ⊥x轴,
则xP=xQ=
,代入椭圆的方程得:P(
,
),Q(
,-
),
把点P坐标代入抛物线方程得:p=
,
∴抛物线C2的通径为
;
(3)10当l的斜率为0时,则
•
=-4;
20当l的斜率存在且不为0时,设l:x=my+1,A(x1,y1),B(x2,y2),
联立
,得(m2+4)y2+2my-3=0,
∴y1+y2=
,y1y2=
,
•
=x1x2+y1y2
=(my1+1)(my2+1)+y1y2=m2y1y2+m(y1+y2)+1+y1y2
=(m2+1)y1y2+m(y1+y2)+1=(m2+1)
+
+1
=
=
=
=-4+
∈(-4,
);
30当l的斜率不存在时,直线方程为x=1,此时A点、B点坐标为(1,
),(1,-
),
故
•
=1×1+
×(-
)=
;
综上可知
•
的取值范围为[-4,
].
| 3 |
| 3 |
且c=
| 3 |
∴曲线C的方程为:
| x2 |
| 4 |
(2)∵
| PF2 |
| F2Q |
则xP=xQ=
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
把点P坐标代入抛物线方程得:p=
| ||
| 24 |
∴抛物线C2的通径为
| ||
| 12 |
(3)10当l的斜率为0时,则
| OA |
| OB |
20当l的斜率存在且不为0时,设l:x=my+1,A(x1,y1),B(x2,y2),
联立
|
∴y1+y2=
| -2m |
| m2+4 |
| -3 |
| m2+4 |
| OA |
| OB |
=(my1+1)(my2+1)+y1y2=m2y1y2+m(y1+y2)+1+y1y2
=(m2+1)y1y2+m(y1+y2)+1=(m2+1)
| -3 |
| m2+4 |
| -2m2 |
| m2+4 |
=
| -3m2-3-2m2+m2+4 |
| m2+4 |
| -4m2+1 |
| m2+4 |
| -4(m2+4)+17 |
| m2+4 |
=-4+
| 17 |
| m2+4 |
| 1 |
| 4 |
30当l的斜率不存在时,直线方程为x=1,此时A点、B点坐标为(1,
| ||
| 2 |
| ||
| 2 |
故
| OA |
| OB |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
综上可知
| OA |
| OB |
| 1 |
| 4 |
点评:本题考查椭圆的定义、方程、性质,考查直线与椭圆的位置关系、向量数量积运算,考查运算求解能力,熟练运用韦达定理是及解决相关问题的基础.

练习册系列答案
相关题目
已知空间四边形ABCD每条边和对角线长都等于a,点E、F、G分别是AB、AD、DC的中点,则a2是下列哪个选项的计算结果( )
A、2
| ||||
B、2
| ||||
C、2
| ||||
D、2
|
1+C271+C272+C2727除以3所得余数为( )
| A、0 | B、1 | C、2 | D、3 |
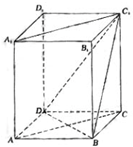 如图,四棱柱ABCD-A1B1C1D1的底面是正方形,且侧棱和底面垂直.
如图,四棱柱ABCD-A1B1C1D1的底面是正方形,且侧棱和底面垂直.