题目内容
已知数列{an}中，an=（2n-1）•3n，求Sn．
考点：数列的求和
专题：等差数列与等比数列
分析：利用“错位相减法”、等比数列的前n项和公式即可得出．
解答：
解：∵an=（2n-1）•3n，
∴Sn=3+3×32+5×33+…+（2n-1）•3n，
∴3Sn=32+3×33+5×34+…+（2n-3）•3n+（2n-1）•3n+1，
∴-2Sn=3+2×32+2×33+…+2×3n-（2n-1）•3n+1=2×
-3-（2n-1）×3n+1=（2-2n）×3n+1-6，
∴Sn=（n-1）×3n+1+3．
∴Sn=3+3×32+5×33+…+（2n-1）•3n，
∴3Sn=32+3×33+5×34+…+（2n-3）•3n+（2n-1）•3n+1，
∴-2Sn=3+2×32+2×33+…+2×3n-（2n-1）•3n+1=2×
| 3(3n-1) |
| 3-1 |
∴Sn=（n-1）×3n+1+3．
点评：本题考查了“错位相减法”、等比数列的前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
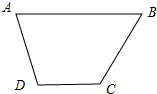如图，等腰梯形ABCD中，AB∥CD，且AB=2，AD=1，DC=2x（x∈（0，1）），以A，B为焦点，且过点D的双曲线的离心率为e1．以C，D为焦点，且过点A的椭圆的离心率为e1，动点E在边AB上，且|AE|＜e1+e2，对x∈（0，1）恒成立，则|AE|的最大值为（ ）
如图，在?ABCD中，E是AD上的一点，且AE=AB，BE和CD的延长线交于点F，且∠BFC=35°，求?ABCD的各内角的度数．