题目内容
已知在△ABC中，∠A、∠B、∠C的对边分别为a、b、c满足2
•
=a2-（b+c）2，求∠A的大小．
| AB |
| AC |
考点：余弦定理,正弦定理
专题：解三角形
分析：利用数量积运算、余弦定理即可得出．
解答：
解：∵2
•
=a2-（b+c）2，
∴2cbcosA=-（b2+c2-a2+2bc）=-2bccosA-2bc，
化为cosA=-
，∵A∈（0，π）．
∴A=
．
| AB |
| AC |
∴2cbcosA=-（b2+c2-a2+2bc）=-2bccosA-2bc，
化为cosA=-
| 1 |
| 2 |
∴A=
| 2π |
| 3 |
点评：本题考查了数量积运算、余弦定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，AB=4，AC=3，∠A=60°，点H是△ABC的垂心，设存在实数λ，μ，使
=λ
+μ
，则（ ）
| AH |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
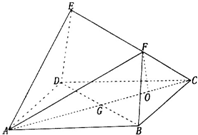如图正方形ABCD的边长为ABCD的边长为2