题目内容
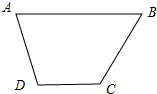 如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( )
如图,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B为焦点,且过点D的双曲线的离心率为e1.以C,D为焦点,且过点A的椭圆的离心率为e1,动点E在边AB上,且|AE|<e1+e2,对x∈(0,1)恒成立,则|AE|的最大值为( )A、
| ||
| B、2 | ||
C、
| ||
| D、不存在 |
考点:双曲线的简单性质
专题:函数的性质及应用,圆锥曲线的定义、性质与方程
分析:根据余弦定理表示出BD,进而根据双曲线的定义可得到a1的值,再由AB=2c1,e=
可表示出e1,同样表示出椭圆中的c2和a2表示出e2的关系式,然后利用换元法求出e1+e2的取值范围,再由恒成立思想即可得到所求最大值.
| c |
| a |
解答:
 解:在等腰梯形ABCD中,BD2=AD2+AB2-2AD•AB•cos∠DAB
解:在等腰梯形ABCD中,BD2=AD2+AB2-2AD•AB•cos∠DAB
=1+4-2×1×2×(1-x)=1+4x,
由双曲线的定义可得a1=
,c1=1,e1=
;
由椭圆的定义可得a2=
,c2=x,e2=
,
则e1+e2=
+
=
+
,
令t=
-1∈(0,
-1),
则e1+e2=
(t+
)在(0,
-1)上递减,
则e1+e2>
×(
-1+
)=
,
则有e1+e2的取值范围为(
,+∞).
由于|AE|<e1+e2,对x∈(0,1)恒成立,
则有|AE|≤
.
即有|AE|的最大值为
.
故选C.
 解:在等腰梯形ABCD中,BD2=AD2+AB2-2AD•AB•cos∠DAB
解:在等腰梯形ABCD中,BD2=AD2+AB2-2AD•AB•cos∠DAB=1+4-2×1×2×(1-x)=1+4x,
由双曲线的定义可得a1=
| ||
| 2 |
| 2 | ||
|
由椭圆的定义可得a2=
| ||
| 2 |
| 2x | ||
|
则e1+e2=
| 2 | ||
|
| 2x | ||
|
| 2 | ||
|
| ||
| 2 |
令t=
| 1+4x |
| 5 |
则e1+e2=
| 1 |
| 2 |
| 4 |
| t |
| 5 |
则e1+e2>
| 1 |
| 2 |
| 5 |
| 4 | ||
|
| 5 |
则有e1+e2的取值范围为(
| 5 |
由于|AE|<e1+e2,对x∈(0,1)恒成立,
则有|AE|≤
| 5 |
即有|AE|的最大值为
| 5 |
故选C.
点评:本题主要考查椭圆的定义和简单性质、双曲线的定义和简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
