题目内容
14.求函数$y=3sinx+2\sqrt{2+2cos2x}$的最大值.分析 利用二倍角公式化简函数的解析式,利用柯西不等式求解函数的最值即可.
解答 解:$y=3sinx+2\sqrt{2+2cos2x}=3sinx+4\sqrt{{{cos}^2}x}$…2分
由柯西不等式得${y^2}={(3sinx+4\sqrt{{{cos}^2}x})^2}≤({3^2}+{4^2})({sin^2}x+{cos^2}x)=25$,…8分
所以ymax=5,此时$sinx=\frac{3}{5}$.
所以函数$y=3sinx+2\sqrt{2+2cos2x}$的最大值为5. …10分.
点评 本题考查是的最值,柯西不等式在最值中的应用,考查转化思想以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.复数(1+i)z=1-i(其中i为虚数单位),则z2等于( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
19.已知复数z满足z(1+i)=1-i,则|z|=( )
| A. | i | B. | 1 | C. | -i | D. | -1 |
3.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{5π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
4.设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),g(x)若的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时,$f(x)=\frac{1}{6}{x^2}-\frac{1}{2}a{x^2}+x$,在x∈(-1,2)上为“凸函数”,则函数f(x)在(-1,2)上结论正确的是( )
| A. | 既有极大值,也有极小值 | B. | 有极大值,没有极小值 | ||
| C. | 没有极大值,有极小值 | D. | 既无极大值,也没有极小值 |

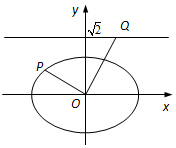 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.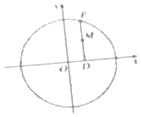 如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.
如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.