题目内容
16.已知函数f(x)=ex+ax+b(a,b∈R)在x=ln2处的切线方程为y=x-2ln2.(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当x>0,k≤2时,求证:(k-x)f'(x)<x+1(其中f'(x)为f(x)的导函数).
分析 (Ⅰ)求出函数的导数,根据f′(ln2)=1,求出a的值,从而求出函数的单调区间;
(Ⅱ)问题转化为(k-x)ex-k-1<0,令g(x)=(k-x)ex-k-1,(x>0),根据函数的单调性证明即可.
解答 解:(Ⅰ)f′(x)=ex+a,
由已知得f′(ln2)=1,故eln2+a=1,解得a=-1,
又f(ln2)=-ln2,得eln2-ln2+b=-ln2,解得:b=-2,
f(x)=ex-x-2,所以f′(x)=ex-1,
当x<0时,f′(x)<0;当x>0时,f′(x)>0,
所以f(x)的单调区间递增区间为(0,+∞),递减区间为(-∞,0);
证明:(Ⅱ)由已知(k-x)f′(x)<x+1,及f′(x)=ex-1,
整理得(k-x)ex-k-1<0,
令g(x)=(k-x)ex-k-1,(x>0),g′(x)=(k-1-x)ex,
g′(x)=0得,x=k-1,
①因为x>0,所以g′(x)<0,g(x)在(0,+∞)上为减函数,
g(x)<g(0)=-1<0,满足条件.
②当1<k≤2时,x∈(0,k-1),g′(x)>0,g(x)在上为增函数;
x∈(k-1,+∞),g′(x)<0,g(x)在上为减函数.
所以g(x)max=g(k-1)=ek-1-(k+1),
令h(k)=ek-1-(k+1),(1<k≤2),h′(k)=ek-1-1>0,
h(k)在k∈(1,2]上为增函数,所以h(k)≤h(2)=e-3<0,
故当x>0,k≤2时,(k-x)f′(x)<x+1成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
( I)求a,b的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合计 | 100 | 1.00 |
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
4.设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),g(x)若的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时,$f(x)=\frac{1}{6}{x^2}-\frac{1}{2}a{x^2}+x$,在x∈(-1,2)上为“凸函数”,则函数f(x)在(-1,2)上结论正确的是( )
| A. | 既有极大值,也有极小值 | B. | 有极大值,没有极小值 | ||
| C. | 没有极大值,有极小值 | D. | 既无极大值,也没有极小值 |
1.已知某几何体的三视图如图所示,则该几何体的体积是( )
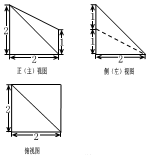

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
6.设集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|y=$\sqrt{{x}^{2}-1}$},则下列结论中正确的是( )
| A. | A=B | B. | A⊆B | C. | B⊆A | D. | A∩B={x|x≥1} |
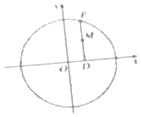 如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.
如图,在圆x2+y2=9上任取一点P,过点P作x轴的垂线PD,D为垂足,点M满足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;当点P在圆x2+y2=9上运动时,点M的轨迹为E.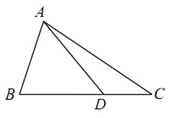 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.