题目内容

14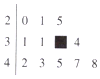．在如图所示一组数据的茎叶图中，有一个数字被污染后而模糊不清，但曾计算得该组数据的极差与中位数之和为61，则被污染的数字为（　　）
A．1B．2C．3D．4

分析 设出被污染的数字为x，根据题意写出中位数与极差，列方程求出x的值即可．

解答 解：设被污染的数字为x，
则该组数据的中位数为$\frac{（30+x）+34}{2}$=$\frac{x}{2}$+32，
极差为48-20=28，
∴（$\frac{x}{2}$+32）+28=61，
解得x=2；
则被污染的数字为2．
故选：B．

点评 本题考查了茎叶图以及中位数和极差的应用问题，是基础题．

练习册系列答案
相关题目
4．设函数f（x）在（m，n）上的导函数为g（x），x∈（m，n），g（x）若的导函数小于零恒成立，则称函数f（x）在（m，n）上为“凸函数”．已知当a≤2时，$f（x）=\frac{1}{6}{x^2}-\frac{1}{2}a{x^2}+x$，在x∈（-1，2）上为“凸函数”，则函数f（x）在（-1，2）上结论正确的是（　　）
A．既有极大值，也有极小值B．有极大值，没有极小值
C．没有极大值，有极小值D．既无极大值，也没有极小值
5．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），椭圆C短轴的一个端点与长轴的一个端点的连线与圆O：x2+y2=$\frac{4}{3}$相切，且抛物线y2=-4$\sqrt{2}$x的准线恰好过椭圆C的一个焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过圆O上任意一点P作圆的切线l与椭圆C交于A，B两点，连接PO并延长交圆O于点Q，求△ABQ面积的取值范围．
2．已知等差数列{an}前n项和为Sn，且${S_n}={n^2}+c$（n∈N*）．
（Ⅰ） 求c，an；
（Ⅱ） 若${b_n}=\frac{a_n}{2^n}$，求数列{bn}前n项和Tn．
9．设数列{an}的前n项和为Sn，且Sn=-1+2an
（Ⅰ）求{an}的通项公式；
（Ⅱ）若bn=log2an+1，且数列{bn}的前n项和为Tn，求$\frac{1}{{T}_{1}}+\frac{1}{{T}_{2}}$+…+$\frac{1}{{T}_{n}}$．
19．某种电路开关闭合后会出现红灯或绿灯闪烁，已知开关第一次闭合后出现红灯的概率为$\frac{1}{2}$，两次闭合后都出现红灯的概率为$\frac{1}{5}$，则在第一次闭合后出现红灯的条件下第二次闭合后出现红灯的概率为（　　）
A．$\frac{1}{10}$B．$\frac{1}{5}$C．$\frac{2}{5}$D．$\frac{1}{2}$
6．设集合A={y|y=$\sqrt{{x}^{2}-1}$}，B={x|y=$\sqrt{{x}^{2}-1}$}，则下列结论中正确的是（　　）
A．A=BB．A⊆BC．B⊆AD．A∩B={x|x≥1}
3．已知抛物线C：y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合，则抛物线C的方程是（　　）
A．y2=2xB．y2=-2xC．y2=4xD．y2=-4x
4．对于函数g（x）=$\left\{\begin{array}{l}{sinπx，x∈（2，+∞）}\\{2g（x+2），x∈（0，2]}\end{array}\right.$，若关于x的方程g（x）=n（n＞0）有且只有两个不同的实根x1，x2，则x1+x2=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网