题目内容
12.已知y=f(x+1)+2是定义域为R的奇函数,则f(e)+f(2-e)=-4.分析 y=f(x+1)+2的图象关于原点(0,0)对称,则 y=f(x)图象关于(1,-2)对称,即可求出f(e)+f(2-e).
解答 解:y=f(x+1)+2的图象关于原点(0,0)对称,
则y=f(x)是由y=f(x+1)+2的图象向右平移1个单位、向下平移2个单位得到,图象关于(1,-2)对称,f(e)+f(2-e)=-4.
故答案为-4.
点评 本题考查函数的奇偶性、对称性,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
3.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{5π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
7.为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
( I)求a,b的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合计 | 100 | 1.00 |
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
17.设集合A={-1,0,1,2},B={x|x-1<0},则A∩B=( )
| A. | (-1,1) | B. | (-1,0) | C. | {-1,0,1} | D. | {-1,0} |
4.设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),g(x)若的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时,$f(x)=\frac{1}{6}{x^2}-\frac{1}{2}a{x^2}+x$,在x∈(-1,2)上为“凸函数”,则函数f(x)在(-1,2)上结论正确的是( )
| A. | 既有极大值,也有极小值 | B. | 有极大值,没有极小值 | ||
| C. | 没有极大值,有极小值 | D. | 既无极大值,也没有极小值 |
1.已知某几何体的三视图如图所示,则该几何体的体积是( )
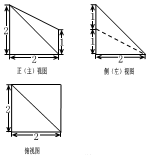

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
