题目内容
13.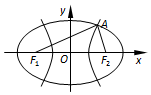 如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点A是C1,C2的公共点.设C1,C2的离心率分别是e1,e2,∠F1AF2=2θ,则( )
如图,F1,F2是椭圆C1与双曲线C2的公共焦点,点A是C1,C2的公共点.设C1,C2的离心率分别是e1,e2,∠F1AF2=2θ,则( )| A. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=e_1^2e_2^2$ | |
| B. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=e_1^2e_2^2$ | |
| C. | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=1$ | |
| D. | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=1$ |
分析 根据椭圆的几何性质可得,${S}_{△P{F}_{1}{F}_{2}}$=b12tanθ,根据双曲线的几何性质可得,${S}_{△P{F}_{1}{F}_{2}}$=$\frac{{b}_{2}^{2}}{tanθ}$,以及离心率以及a,b,c的关系即可求出答案.
解答 解:根据椭圆的几何性质可得,${S}_{△P{F}_{1}{F}_{2}}$=b12tanθ,
∵e1=$\frac{c}{{a}_{1}}$,
∴a1=$\frac{c}{{e}_{1}}$,
∴b12=a12-c2=$\frac{{c}^{2}}{{e}_{1}^{2}}$-c2,
∴${S}_{△P{F}_{1}{F}_{2}}$=c2($\frac{1-{e}_{1}^{2}}{{e}_{1}^{2}}$)tanθ
根据双曲线的几何性质可得,${S}_{△P{F}_{1}{F}_{2}}$=$\frac{{b}_{2}^{2}}{tanθ}$,
∵a2=$\frac{c}{{e}_{2}}$,
∴b22=c2-a22=c2-$\frac{{c}^{2}}{{e}_{2}^{2}}$=c2($\frac{{e}_{2}^{2}-1}{{e}_{2}^{2}}$)
∴${S}_{△P{F}_{1}{F}_{2}}$=c2($\frac{{e}_{2}^{2}-1}{{e}_{2}^{2}}$)•$\frac{1}{tanθ}$,
∴c2($\frac{1-{e}_{1}^{2}}{{e}_{1}^{2}}$)tanθ=c2($\frac{{e}_{2}^{2}-1}{{e}_{2}^{2}}$)•$\frac{1}{tanθ}$,
∴($\frac{1-{e}_{1}^{2}}{{e}_{1}^{2}}$)sin2θ=($\frac{{e}_{2}^{2}-1}{{e}_{2}^{2}}$)•cos2θ,
∴${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=e_1^2e_2^2$,
故选:B
点评 本题考查了圆锥曲线的几何性质,以及椭圆和双曲线的简单性质,属于中档题.

 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{6}V$ | B. | $\frac{1}{12}V$ | C. | $\frac{1}{16}V$ | D. | $\frac{1}{24}V$ |
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |
| A. | l1⊥l2 | B. | l1∥l2 | ||
| C. | l1与l2相交不平行 | D. | l1与l2重合 |