题目内容
3．直线l1、l2的方向向量分别为$\vec a=（1，-3，-1）$，$\vec b=（8，2，2）$，则（ ）| A． | l1⊥l2 | B． | l1∥l2 | ||
| C． | l1与l2相交不平行 | D． | l1与l2重合 |
分析 由直线l1、l2的方向向量分别为$\vec a=（1，-3，-1）$，$\vec b=（8，2，2）$，得到1×8-3×2-1×2=0，即可得出结论．
解答 解：∵直线l1、l2的方向向量分别为$\vec a=（1，-3，-1）$，$\vec b=（8，2，2）$，
∴1×8-3×2-1×2=0，
∴l1⊥l2．
故选A．
点评 本题考查直线的方向向量，考查向量的数量积公式，比较基础．
练习册系列答案
中考解读考点精练系列答案
相关题目
13．
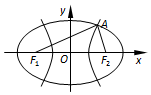如图，F1，F2是椭圆C1与双曲线C2的公共焦点，点A是C1，C2的公共点．设C1，C2的离心率分别是e1，e2，∠F1AF2=2θ，则（ ）
如图，F1，F2是椭圆C1与双曲线C2的公共焦点，点A是C1，C2的公共点．设C1，C2的离心率分别是e1，e2，∠F1AF2=2θ，则（ ）| A． | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=e_1^2e_2^2$ | |
| B． | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=e_1^2e_2^2$ | |
| C． | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=1$ | |
| D． | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=1$ |
14．若sinα+$\sqrt{3}$cosα=2，则tan（π+α）=（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
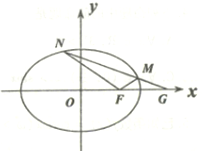已知椭圆$Ω：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$，直线$\frac{{\sqrt{2}}}{2}x+y=1$经过Ω的右顶点和上顶点．
15．设集合A={x|x2-x-6＞0}，B={x|-3≤x≤1}，则A∩B=（ ）
| A． | （-2，1] | B． | （-3，-2] | C． | [-3，-2） | D． | （-∞，1]∪（3，+∞） |