题目内容
8．设三棱柱ABC-A1B1C1体积为V，E，F，G分别是AA1，AB，AC的中点，则三棱锥E-AFG体积是（ ）| A． | $\frac{1}{6}V$ | B． | $\frac{1}{12}V$ | C． | $\frac{1}{16}V$ | D． | $\frac{1}{24}V$ |
分析 由E，F，G分别是AA1，AB，AC的中点，知S△AFG=$\frac{1}{4}{S}_{△ABC}$，$AE=\frac{1}{2}A{A}_{1}$，由此能求出三棱锥E-AFG体积．
解答 解：∵三棱柱ABC-A1B1C1体积为V，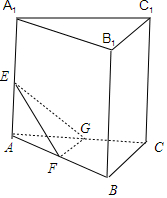
∴V=S△ABC•AA1，
∵E，F，G分别是AA1，AB，AC的中点，
∴S△AFG=$\frac{1}{4}{S}_{△ABC}$，$AE=\frac{1}{2}A{A}_{1}$，
∴三棱锥E-AFG体积：
VE-AFG=$\frac{1}{3}×{S}_{△AFG}×AE$=$\frac{1}{3}×（\frac{1}{4}{S}_{△ABC}）×（\frac{1}{2}A{A}_{1}）$=$\frac{1}{24}$S△ABC•AA1=$\frac{1}{24}V$．
故选：D．
点评 本题考查三棱锥的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
18．设集合A={x|2x≤8}，B={x|x≤m2+m+1}，若A∪B=A，则实数m的取值范围为．（ ）
| A． | [-2，1） | B． | [-2，1] | C． | [-2，-1） | D． | [-1，1） |
13．
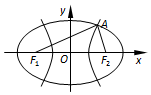如图，F1，F2是椭圆C1与双曲线C2的公共焦点，点A是C1，C2的公共点．设C1，C2的离心率分别是e1，e2，∠F1AF2=2θ，则（ ）
如图，F1，F2是椭圆C1与双曲线C2的公共焦点，点A是C1，C2的公共点．设C1，C2的离心率分别是e1，e2，∠F1AF2=2θ，则（ ）| A． | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=e_1^2e_2^2$ | |
| B． | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=e_1^2e_2^2$ | |
| C． | ${e_2}^2{sin^2}θ+{e_1}^2{cos^2}θ=1$ | |
| D． | ${e_1}^2{sin^2}θ+{e_2}^2{cos^2}θ=1$ |
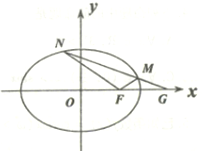已知椭圆$Ω：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$，直线$\frac{{\sqrt{2}}}{2}x+y=1$经过Ω的右顶点和上顶点．