题目内容
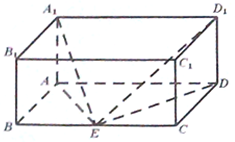 如图,长方体ABCD-A1B1C1D1中,AB=AA1=1,AD=2,E是BC的中点
如图,长方体ABCD-A1B1C1D1中,AB=AA1=1,AD=2,E是BC的中点(1)求证:平面A1AE⊥D1DE平面;
(2)求三棱锥A-D1DE的体积;
(3)求点A1到平面D1DE的距离.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定,点、线、面间的距离计算
专题:计算题,证明题,空间位置关系与距离
分析:(1)由AE⊥ED,AE⊥DD1证明平面A1AE⊥D1DE平面;
(2)确定底面D1DE与高AE,求三棱锥A-D1DE的体积;
(3)点A1到平面D1DE的距离等于点A到平面D1DE的距离.
(2)确定底面D1DE与高AE,求三棱锥A-D1DE的体积;
(3)点A1到平面D1DE的距离等于点A到平面D1DE的距离.
解答:
解:(1)证明:在矩形ABCD中,E是BC的中点,AB=1,AD=2,
则∠AEB=∠DEC=45°
则AE⊥ED,
又∵AE⊥DD1;
则AE⊥平面D1DE;
∴平面A1AE⊥平面D1DE;
(2)AE=ED=
,
S△D1DE=
•
•1=
,
h=
,
V=
•S•h=
•
•
=
,
(3)∵AA1∥平面D1DE,
∴点A1到平面D1DE的距离等于点A到平面D1DE的距离;
∴点A1到平面D1DE的距离为
.
则∠AEB=∠DEC=45°
则AE⊥ED,
又∵AE⊥DD1;
则AE⊥平面D1DE;
∴平面A1AE⊥平面D1DE;
(2)AE=ED=
| 2 |
S△D1DE=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
h=
| 2 |
V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 2 |
| 1 |
| 3 |
(3)∵AA1∥平面D1DE,
∴点A1到平面D1DE的距离等于点A到平面D1DE的距离;
∴点A1到平面D1DE的距离为
| 2 |
点评:本题考查了面面垂直的判定及三棱锥的体积求法,同时考查了转化的思想,属于中档题.

练习册系列答案
相关题目
 在如图所示的几何体中,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,BC⊥AB,PO=OB=BC=CD,EA=AO=
在如图所示的几何体中,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,BC⊥AB,PO=OB=BC=CD,EA=AO= 随机抽取某中学高一年级学生的一次数学统测成绩得到一样本,其分组区间和频数:[50,60),2:[60,70),7:[70,80),10:[80,90),x[90,100],2,其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题:
随机抽取某中学高一年级学生的一次数学统测成绩得到一样本,其分组区间和频数:[50,60),2:[60,70),7:[70,80),10:[80,90),x[90,100],2,其频率分布直方图受到破坏,可见部分如图所示,据此解答如下问题: 某校高二年纪在依次数学必修模块考试后随机抽取40名学生的成绩,按成绩共分为五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),得到的频率直方图如图所示,同时规定成绩在90分以上的记为A级,成绩小于90分的记为B级.
某校高二年纪在依次数学必修模块考试后随机抽取40名学生的成绩,按成绩共分为五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),得到的频率直方图如图所示,同时规定成绩在90分以上的记为A级,成绩小于90分的记为B级. 在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的正方形,AA1=2,点E、M分别为A1B,C1C的中点,过点A1、B、M三点的平面ABMN与棱C1D1相交于点N
在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的正方形,AA1=2,点E、M分别为A1B,C1C的中点,过点A1、B、M三点的平面ABMN与棱C1D1相交于点N