题目内容
 在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的正方形,AA1=2,点E、M分别为A1B,C1C的中点,过点A1、B、M三点的平面ABMN与棱C1D1相交于点N
在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的正方形,AA1=2,点E、M分别为A1B,C1C的中点,过点A1、B、M三点的平面ABMN与棱C1D1相交于点N(1)求证:EM∥平面A1B1C1D1
(2)求三棱锥A1-DEM的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:计算题,证明题,空间位置关系与距离
分析:(1)取A1B1的中点F,连EF,C1F;证明EF∥C1M,从而EM∥平面A1B1C1D1;(2)体积转化,三棱锥A1-DEM的体积等于三棱锥A1-NDM的体积.
解答:
解:(Ⅰ)(方法1 )证明:取A1B1的中点F,连EF,C1F
∵E为A1B中点∴EF∥
BB1
又∵M为CC1中点∴EF∥C1M
∴四边形EFC1M为平行四边形∴EM∥FC1
而EM?平面A1B1C1D1,FC1?平面A1B1C1D1
∴EM∥平面A1B1C1D1
(方法2 )可以证明四边形A1EMN为平行四边形.

(Ⅱ) 由(Ⅰ)可得EM∥A1N又MN∥A1E
∴四边形A1EMN为平行四边形.
∴N点和E点到平面A1DM的距离相等.
∴VA1-DEM=VE-A1DM
=VN-A1DM=VA1-NDM;
S△NDM=2•4-
•22-
•2•1-
•4•1=3.
VA1-EDM=VA1-NDM=
•3•4=4
∵E为A1B中点∴EF∥
| 1 |
| 2 |
又∵M为CC1中点∴EF∥C1M
∴四边形EFC1M为平行四边形∴EM∥FC1
而EM?平面A1B1C1D1,FC1?平面A1B1C1D1
∴EM∥平面A1B1C1D1
(方法2 )可以证明四边形A1EMN为平行四边形.

(Ⅱ) 由(Ⅰ)可得EM∥A1N又MN∥A1E
∴四边形A1EMN为平行四边形.
∴N点和E点到平面A1DM的距离相等.
∴VA1-DEM=VE-A1DM
=VN-A1DM=VA1-NDM;
S△NDM=2•4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
VA1-EDM=VA1-NDM=
| 1 |
| 3 |
点评:考查了线面平行的判定定理及体积的转化思想,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
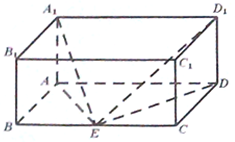 如图,长方体ABCD-A1B1C1D1中,AB=AA1=1,AD=2,E是BC的中点
如图,长方体ABCD-A1B1C1D1中,AB=AA1=1,AD=2,E是BC的中点 如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为A1B1的中点.
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为A1B1的中点.