题目内容
已知在直角坐标系xOy中，直线l的参数方程为
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2-4ρcosθ+3=0．点P在直线l上，点Q在曲线C上，求PQ的取值范围．
|
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把参数方程、极坐标方程化为直角坐标方程，求出圆心到直线的距离，再将此距离减去半径，可得PQ的最小值，而PQ没有最大值，从而求得PQ的取值范围．
解答：
解：直线l的普通方程为：4x-3y+8=0，
曲线的直角坐标方程为（x-2）2+y2=1，
曲线C是圆心为（2，0），半径为1的圆，
圆心到直线的距离是d=
=
，
所以PQ的取值范围是[
，+∞]．
曲线的直角坐标方程为（x-2）2+y2=1，
曲线C是圆心为（2，0），半径为1的圆，
圆心到直线的距离是d=
| |4×2-0+8| |
| 5 |
| 16 |
| 5 |
所以PQ的取值范围是[
| 11 |
| 5 |
点评：本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，直线和圆的位置关系，属于基础题．
练习册系列答案
相关题目
已知抛物线的顶点在坐标原点O，开口向上，等腰梯形ABCD下底AB的中点与坐标原点重合，上底DC∥x轴，等腰梯形的高是3，线段DC与抛物线相交于S，R，且SR=4，DA、AB、BC，分别于抛物线相切于点P、O、Q（如图所示）
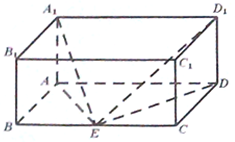如图，长方体ABCD-A1B1C1D1中，AB=AA1=1，AD=2，E是BC的中点