题目内容
已知A（1，0），B（-1，0），P是平面上的一个动点，且满足|
|•|
|=
•
，
（1）求点P的轨迹方程；
（2）若直线y=x+m（m≠0）与点P的轨迹交于M，N两点，且
⊥
，求m．
| PA |
| AB |
| PB |
| AB |
（1）求点P的轨迹方程；
（2）若直线y=x+m（m≠0）与点P的轨迹交于M，N两点，且
| OM |
| ON |
考点：轨迹方程,数量积判断两个平面向量的垂直关系
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）利用向量的数量积公式，即可求点P的轨迹方程；
（2）直线y=x+m代入抛物线方程，利用
⊥
，可得x1x2+y1y2=0，即可求m．
（2）直线y=x+m代入抛物线方程，利用
| OM |
| ON |
解答：
解：（1）设P（x，y），则
∵A（1，0），B（-1，0），|
|•|
|=
•
，
∴2
=2（x+1），即y2=4x；
（2）设M（x1，y1），N（x2，y2），
则直线y=x+m代入抛物线方程可得x2+（2m-4）x+m2=0，则x1+x2=4-2m，x1x2=m2，
∵△＞0，∴m＜1，
∵
⊥
，
∴x1x2+y1y2=x1x2+（x1+m）（x2+m）=m2+4m=0，
∴m=0或-4，
∵m＜1且m≠0，
∴m=-4．
∵A（1，0），B（-1，0），|
| PA |
| AB |
| PB |
| AB |
∴2
| (x-1)2+y2 |
（2）设M（x1，y1），N（x2，y2），
则直线y=x+m代入抛物线方程可得x2+（2m-4）x+m2=0，则x1+x2=4-2m，x1x2=m2，
∵△＞0，∴m＜1，
∵
| OM |
| ON |
∴x1x2+y1y2=x1x2+（x1+m）（x2+m）=m2+4m=0，
∴m=0或-4，
∵m＜1且m≠0，
∴m=-4．
点评：本题考查抛物线方程，考查直线与抛物线的位置关系，考查向量知识的运用，属于中档题．
练习册系列答案
相关题目
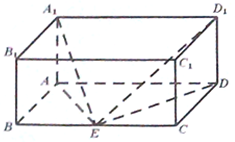如图，长方体ABCD-A1B1C1D1中，AB=AA1=1，AD=2，E是BC的中点