题目内容
函数f（x）=sinxsin（
-x）的最小正周期为（ ）
| π |
| 2 |
| A、π | ||
B、
| ||
C、
| ||
| D、2π |
考点：三角函数的周期性及其求法,二倍角的正弦
专题：三角函数的图像与性质
分析：利用诱导公式与二倍角的正弦可得f（x）=
sin2x，从而可求其最小正周期．
| 1 |
| 2 |
解答：
解：f（x）=sinxsin（
-x）=sinxcosx=
sin2x，
其周期T=
=π，
故选：A．
| π |
| 2 |
| 1 |
| 2 |
其周期T=
| 2π |
| 2 |
故选：A．
点评：本题考查二倍角的正弦及诱导公式，考查三角函数的周期性及其求法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
△ABC中，若a2-b2=
bc，sinC=2
sinB，则A=（ ）
| 3 |
| 3 |
| A、150° | B、60° |
| C、120° | D、30° |
在复平面内，复数
+（1+i）2对应的点位于（ ）
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知变量x，y满足约束条件
，则z=2x+y的最大值是（ ）
|
| A、-3 | ||
B、
| ||
| C、3 | ||
| D、5 |
在如图所示的正方形中随机掷一粒豆子，豆子落在正方形内切圆的上半圆（图中阴影部分）中的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
设随机变量ξ服从正态分布N（0，1），P（ξ＞1）=p，则P（-1＜ξ＜0）等于（ ）
A、
| ||
| B、1-p | ||
| C、1-2p | ||
D、
|
满足a∈A且4-a∈A，a∈N且4-a∈N，有且只有2个元素的集合A的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
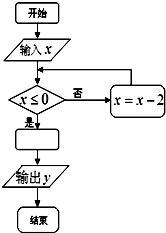如图是一个算法程序框图，当输入的x值为3时，输出的结果恰好是| 1 |
| 3 |
A、y=x -
| ||
B、y=x
| ||
| C、y=3-x | ||
| D、y=3x |