题目内容
1.若函数exf(x)(e≈2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数的序号为①④.①f(x)=2-x ②f(x)=3-x ③f(x)=x3 ④f(x)=x2+2.
分析 把①②代入exf(x),变形为指数函数判断;把③④代入exf(x),求导数判断.
解答 解:对于①,f(x)=2-x,则g(x)=exf(x)=${e}^{x}•{2}^{-x}=(\frac{e}{2})^{x}$为实数集上的增函数;
对于②,f(x)=3-x,则g(x)=exf(x)=${e}^{x}•{3}^{-x}=(\frac{e}{3})^{x}$为实数集上的减函数;
对于③,f(x)=x3,则g(x)=exf(x)=ex•x3,
g′(x)=ex•x3+3ex•x2=ex(x3+3x2)=ex•x2(x+3),当x<-3时,g′(x)<0,
∴g(x)=exf(x)在定义域R上先减后增;
对于④,f(x)=x2+2,则g(x)=exf(x)=ex(x2+2),
g′(x)=ex(x2+2)+2xex=ex(x2+2x+2)>0在实数集R上恒成立,
∴g(x)=exf(x)在定义域R上是增函数.
∴具有M性质的函数的序号为①④.
故答案为:①④.
点评 本题考查函数单调性的性质,训练了利用导数研究函数的单调性,是中档题.

练习册系列答案
相关题目
7.若x=-2是函数f(x)=(x2+ax-1)ex-1的极值点,则f(x)的极小值为( )
| A. | -1 | B. | -2e-3 | C. | 5e-3 | D. | 1 |
12.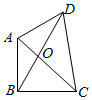 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )| A. | I1<I2<I3 | B. | I1<I3<I2 | C. | I3<I1<I2 | D. | I2<I1<I3 |
9.设函数y=$\sqrt{4-{x}^{2}}$的定义域为A,函数y=ln(1-x)的定义域为B,则A∩B=( )
| A. | (1,2) | B. | (1,2] | C. | (-2,1) | D. | [-2,1) |
16.从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到在2张卡片上的数奇偶性不同的概率是( )
| A. | $\frac{5}{18}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F,离心率为$\sqrt{2}$.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}$=1 |
10.设x∈R,则“2-x≥0”是“|x-1|≤1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.已知函数$f(x)=\left\{\begin{array}{l}{2^x}\\ log_2^x\end{array}\right.$$\begin{array}{l}x≤0\\ x>0\end{array}$,若$f(a)=\frac{1}{2}$,则a=( )
| A. | -1 | B. | -1或$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | -1或$-\sqrt{2}$ |