点A关于点B的对称点为A′.若$\overrightarrow{OA}$=$\overrightarrow{a}$.$\overrightarrow{OB}$=$\overrightarrow{b}$.用$\overrightarrow{a}$.$\overrightarrow{b}$表示$\overrightarrow{OA′}$=2$\overrightarrow{b}$-$\overrightarrow 题目和参考答案——青夏教育精英家教网——

题目内容

13．点A关于点B的对称点为A′，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{OA′}$=2$\overrightarrow{b}$-$\overrightarrow{a}$．

分析由A，A′关于B对称可得AB=A′B．根据向量加法的三角形法则得出$\overrightarrow{OA′}$．

解答解：∵A，A′关于B对称，
∴$\overrightarrow{AA′}$=2$\overrightarrow{AB}$=2（$\overrightarrow{OB}-\overrightarrow{OA}$），
∴$\overrightarrow{OA′}$=$\overrightarrow{OA}+\overrightarrow{AA′}$=$\overrightarrow{OA}+2\overrightarrow{OB}-2\overrightarrow{OA}$=2$\overrightarrow{OB}-\overrightarrow{OA}$=2$\overrightarrow{b}-\overrightarrow{a}$．
故答案为2$\overrightarrow{b}-\overrightarrow{a}$．

点评本题考查了平面向量线性运算的几何意义，属于基础题．

练习册系列答案

红领巾乐园系列答案

初中英语最佳方案冲刺AB卷系列答案

新中考指南系列答案

快乐起跑线期末冲刺系列答案

快乐起跑线周考卷系列答案

快乐起跑线单元滚动活页测系列答案

快乐学习一点通系列答案

智慧翔课时导学案系列答案

随堂演练系列答案

中考一本通系列答案

相关题目

3．已知{a_n}是等差数列，且a₁，a₂，a₅成等比数列，a₃+a₄=12．
（1）求a₁+a₂+a₃+a₄+a₅；
（2）设b_n=10-a_n，数列{b_n}的前n项和为S_n，若b₁≠b₂，则n为何值时，S_n最大？S_n最大值是多少？

在正三棱柱ABC-A₁B₁C₁中，AB=$\sqrt{2}$AA₁，求证：BC₁=AB₁．

1．直线m：x+（a²-1）y+1=0，直线n：x+（2-2a）y-1=0，则“a=-3”是“直线m、n关于原点对称”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充分必要条件		D．	既不充分也不必要条件

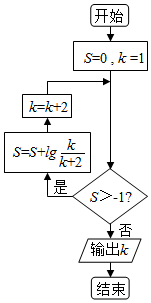
8．执行如图所示的程序框图，输出k的值为（　　）

18．将函数f（x）=sin2x的图象向左平移$\frac{π}{6}$个单位后与函数g（x）的图象重合，则函数g（x）为（　　）

$sin（2x-\frac{π}{6}）$

$sin（2x+\frac{π}{6}）$

$sin（2x-\frac{π}{3}）$

$sin（2x+\frac{π}{3}）$

5．复数z满足z（1-i）=|1+i|，则复数z的共轭复数在复平面内的对应点位于（　　）

2．定义A°B={x|x∈A或x∈B，但x∉A∩B}．已知M={y|y=2^|x|}，N={x|$\frac{3}{2-x}$≤2}，则M°N=（　　）

[0，1）∪（2，+∞）

（-∞，$\frac{1}{2}$]∪[1，2]

[$\frac{1}{2}$，1）∪（2，+∞）

3．已知过抛物线y²=4x的焦点F作直线l交抛物线于A，B两点，若$\overrightarrow{BF}$=2$\overrightarrow{FA}$，则点A的横坐标为（　　）