题目内容
18．将函数f（x）=sin2x的图象向左平移$\frac{π}{6}$个单位后与函数g（x）的图象重合，则函数g（x）为（ ）| A． | $sin（2x-\frac{π}{6}）$ | B． | $sin（2x+\frac{π}{6}）$ | C． | $sin（2x-\frac{π}{3}）$ | D． | $sin（2x+\frac{π}{3}）$ |
分析 利用左加右减的原则，直接推出平移后的函数解析式即可．
解答 解：将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位后所得到的函数图象对应的解析式为：y=sin[2（x+$\frac{π}{6}$）]=sin（2x+$\frac{π}{3}$）．
则函数g（x）为：y=3sin（2x+$\frac{π}{3}$）．
故选：D．
点评 本题考查三角函数的图象变换，注意平移变换中x的系数为1，否则容易出错误，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
8．设Sn是等差数列{an}的前n项和，且满足等式S7=a5+a6+a8+a9，则$\frac{{a}_{7}}{{a}_{4}}$的值为（ ）
| A． | $\frac{7}{4}$ | B． | $\frac{4}{7}$ | C． | $\frac{7}{8}$ | D． | $\frac{8}{7}$ |
9．
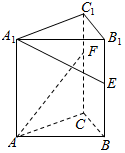如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{2}}{6}$ | C． | $\frac{\sqrt{3}}{10}$ | D． | $\frac{\sqrt{2}}{10}$ |
3．已知命题：p“?x0∈R，x02+2ax0+a≤0”为假命题，则实数a的取值范围是（ ）
| A． | （0，1） | B． | [0，1] | C． | （1，2） | D． | （-∞，0）∪（1，+∞） |
10．命题p：直线l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0互为平行的充要条件是a=-2；命题q：若平面α内存在不共线的三点到平面β的距离相等，则α∥β．对以上两个命题，下列结论正确的是（ ）
| A． | 命题“p且q”为真 | B． | 命题“p或￢q”为假 | C． | 命题“￢p且q”为真 | D． | 命题“p或q”为假 |