题目内容
1．直线m：x+（a2-1）y+1=0，直线n：x+（2-2a）y-1=0，则“a=-3”是“直线m、n关于原点对称”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 在直线m：x+（a2-1）y+1=0上任取点P（x，y），则点P关于原点对称的点Q（-x，-y）在直线n上，代入比较即可得出．
解答 解：在直线m：x+（a2-1）y+1=0上任取点P（x，y），则点P关于原点对称的点Q（-x，-y）在直线n上，
∴-x+（2-2a）（-y）-1=0，化为x+（2-2a）y+1=0，与x+（a2-1）y+1=0比较，可得：a2-1=2-2a，解得a=-3或a=1．
则“a=-3”是“直线m、n关于原点对称”的充分不必要条件．
故选：A．
点评 本题考查了直线关于点的对称性、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
11．命题“若a2＜b，则-$\sqrt{b}$＜a＜$\sqrt{b}$”的逆否命题为（ ）
| A． | 若a2≥b，则a≥$\sqrt{b}$或a≤-$\sqrt{b}$ | B． | 若a2≥b，则a＞$\sqrt{b}$或a＜-$\sqrt{b}$ | ||
| C． | 若a≥$\sqrt{b}$或a≤-$\sqrt{b}$，则a2≥b | D． | 若a＞$\sqrt{b}$或a＜-$\sqrt{b}$，则a2≥b |
12．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线截圆M：（x-1）2+y2=1所得弦长为$\sqrt{3}$，则该双曲线的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{2}{3}$$\sqrt{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{5}{3}$ |
9．
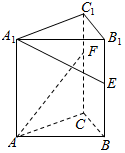如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{2}}{6}$ | C． | $\frac{\sqrt{3}}{10}$ | D． | $\frac{\sqrt{2}}{10}$ |
16．直线2ax+（a2+1）y-1=0的倾斜角的取值范围是（ ）
| A． | [$\frac{π}{4}$，$\frac{3π}{4}$] | B． | [0，$\frac{π}{4}$]∪[$\frac{3π}{4}$，π] | C． | （0，$\frac{π}{4}$]∪[$\frac{3π}{4}$，π） | D． | [0，$\frac{π}{4}$]∪[$\frac{3π}{4}$，π） |
10．命题p：直线l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0互为平行的充要条件是a=-2；命题q：若平面α内存在不共线的三点到平面β的距离相等，则α∥β．对以上两个命题，下列结论正确的是（ ）
| A． | 命题“p且q”为真 | B． | 命题“p或￢q”为假 | C． | 命题“￢p且q”为真 | D． | 命题“p或q”为假 |
11．下列命题是假命题的是（ ）
| A． | ?θ∈R，函数f（x）=-2cos（3x+θ）是奇函数 | |
| B． | “?x∈R，x2+1≥0”的否定是“?x0∈R，x02+1＜0” | |
| C． | 数列{（n+2）（$\frac{9}{10}$）n}的最大项是第7项 | |
| D． | “-1＜x＜0”是“x＜0”的充分不必要条件 |