题目内容
已知x,y满足约束条件
,则z=2x+y的最小值为( )
|
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,代入目标函数得答案.
解答:
解:由约束条件
作出可行域如图,

由图可知A(2,0),
化目标函数z=2x+y为y=-2x+z,
当直线y=-2x+z过A(2,0)时直线在y轴上的截距最小,z有最小值为2×2+0=4.
故答案为:4.
|

由图可知A(2,0),
化目标函数z=2x+y为y=-2x+z,
当直线y=-2x+z过A(2,0)时直线在y轴上的截距最小,z有最小值为2×2+0=4.
故答案为:4.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
圆锥的表面积公式( )
| A、S=πr2+πrl |
| B、S=2πr2+2πrl |
| C、S=πrl |
| D、S=πr2+πR2+πrl+πRl |
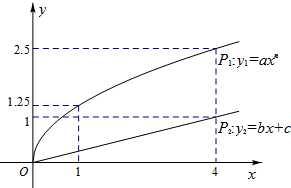 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?