题目内容
命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是( )
| A、使用了归纳推理 |
| B、使用了类比推理 |
| C、使用了“三段论”,但推理形式错误 |
| D、使用了“三段论”,但小前提错误 |
考点:演绎推理的基本方法
专题:推理和证明
分析:本题考查的知识点是演绎推理的基本方法及整数的,在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“有些…”,不难得到结论.
解答:
解:∵大前提的形式:“有些有理数是无限循环小数”,不是全称命题,
∴不符合三段论推理形式,
∴推理形式错误,
故选C.
∴不符合三段论推理形式,
∴推理形式错误,
故选C.
点评:演绎推理的主要形式就是由大前提、小前提推出结论的三段论推理.三段论推理的依据用集合论的观点来讲就是:若集合M的所有元素都具有性质P,S是M的子集,那么S中所有元素都具有性质P.三段论的公式中包含三个判断:第一个判断称为大前提,它提供了一个一般的原理;第二个判断叫小前提,它指出了一个特殊情况;这两个判断联合起来,揭示了一般原理和特殊情况的内在联系,从而产生了第三个判断结论.演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
下列说法正确的是( )
| A、若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处就没有切线 |
| B、若曲线y=f(x)在点(x0,f(x0))处有切线,则f′(x0)必存在 |
| C、若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处的切线斜率不存在 |
| D、若曲线y=f(x)在点(x0,f(x0))处的切线斜率不存在,则曲线在该点处就没有切线 |
一几何体的正视图和侧视图是边长为2的等边三角形,俯视图是直径为2的圆,则此几何体的表面积为( )

A、4π+2
| ||
B、2π+2
| ||
| C、3π | ||
| D、2π |
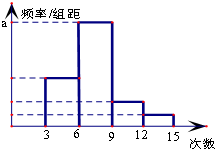 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: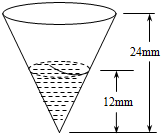 “降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为
“降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为