题目内容
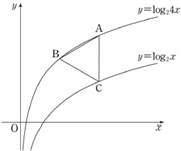 如图所示,已知函数 y=log24x图象上的两点 A、B 和函数 y=log2x上的点 C,线段 AC平行于 y 轴,三角形 ABC 为正三角形时,点B的坐标为 (p,q),则 p2×2q的值为
如图所示,已知函数 y=log24x图象上的两点 A、B 和函数 y=log2x上的点 C,线段 AC平行于 y 轴,三角形 ABC 为正三角形时,点B的坐标为 (p,q),则 p2×2q的值为考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据题意,设出A、B、C的坐标,由线段AC∥y轴,△ABC是等边三角形,得出AB、AC与BC的关系,求出p、q的值,计算出结果.
解答:
解:根据题意,设A(x0,2+log2x0),B(p,q),C(x0,log2x0),
∵线段AC∥y轴,△ABC是等边三角形,
∴AC=2,2+log2p=q,
∴p=2q-2,∴4p=2q;
又x0-p=
,∴p=x0-
,
∴x0=p+
;
又2+log2x0-q=1,
∴log2x0=q-1,x0=2q-1=
;
∴p+
=
,2p+2
=2q=4p,
∴p=
,2q=4
;
∴p2•2q=3×4
=12
.
故答案为:12
.
∵线段AC∥y轴,△ABC是等边三角形,
∴AC=2,2+log2p=q,
∴p=2q-2,∴4p=2q;
又x0-p=
| 3 |
| 3 |
∴x0=p+
| 3 |
又2+log2x0-q=1,
∴log2x0=q-1,x0=2q-1=
| 2q |
| 2 |
∴p+
| 3 |
| 2q |
| 2 |
| 3 |
∴p=
| 3 |
| 3 |
∴p2•2q=3×4
| 3 |
| 3 |
故答案为:12
| 3 |
点评:本题考查了指数函数与对数函数的图象与性质的应用问题,也考查了指数,对数的运算问题,是较难的题目.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的表面积为( )


A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
分别在两个平面内的两条直线的位置关系是( )
| A、异面 | B、相交 |
| C、平行 | D、以上都有可能 |
若角α的顶点与原点重合,始边与x轴的正半轴重合.终边在射线3x+4y=0(x>0)上,则sinα等于( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
不等式x2-3x+2<0的解集是( )
| A、{x|x>2} |
| B、{x|x>1} |
| C、{x|1<x<2} |
| D、{x|x<1或x>2} |