Question

12．若函数f（x）的图象与函数y=（x-2）e^2-x的图象关于点（1，0）对称，且方程f（x）=mx² 只有一个实根，则实数m的取值范围为（　　）

• A． [0，e）
• B． （-∞，e）
• C． {e}
• D． （-∞，0）∪{e}

Answer 1

分析 求出f（x）的解析式，作出f（x）的函数图象，根据f（x）与y=mx²的交点个数判断．

解答 解：∵f（x）的图象与函数y=（x-2）e^2-x的图象关于点（1，0）对称，
∴f（x）=-[（2-x）-2]e^2-（2-x）=xe^x，
f′（x）=e^x（x+1），
∴当x＜-1时，f′（x）＜0，当x＞-1时，f′（x）＞0，
∴f（x）在（-∞，-1）上单调递减，在（-1，+∞）上单调递增，
作出f（x）的函数图象如图所示：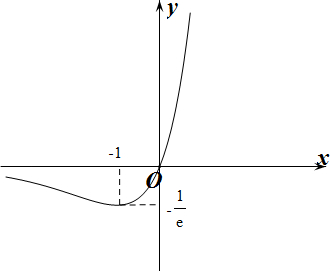

显然，当m=0时，f（x）与y=mx²有1个交点，符合题意；排除C，D；
当m＜0时，抛物线y=mx²与f（x）的图象有2个交点，即f（x）=mx²有2个根，不符合题意，排除B，
故选：A．

点评 本题考查了方程的根与函数图象的关系，函数的单调性判断，属于中档题．