题目内容
6.下列说法正确的是( )| A. | “若a>1,则a2>1”的否命题是“若a>1,则a2≤1” | |
| B. | 在△ABC中,“A>B”是“sin2A>sin2B”必要不充分条件 | |
| C. | “若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 | |
| D. | ?x0∈(-∞,0)使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立 |
分析 A,命题的否定既要否定条件又要否定结论;
B,在△ABC中,“A>B”⇒a>b⇒a2>b2⇒(2RsinA)2>(2RsinB)2⇒sin2A>sin2B,反之亦然;
C,若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$+kπ⇒$α≠\frac{π}{3}$;
D,?x0∈(-∞,0)使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立;
解答 解:对于A,命题的否定既要否定条件又要否定结论,故错;
对于B,在△ABC中,“A>B”⇒a>b⇒a2>b2⇒(2RsinA)2>(2RsinB)2⇒sin2A>sin2B,反之亦然,应是充要分条件,故错;
对于C,若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$+kπ⇒$α≠\frac{π}{3}$,故正确;
对于D,?x0∈(-∞,0)使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立,故错;
故选:C
点评 本题考查了命题真假的判定,涉及到了大量的基础知识,属于基础题.

练习册系列答案
相关题目
11.设函数f(x)=$\left\{\begin{array}{l}{x-2,x≥1}\\{2,x<1}\end{array}\right.$,则满足xf(x-1)≥10的x取值范围为[5,+∞).
18.用二分法研究函数f(x)=x3-2x-1的理念时,若零点所在的初始区间为(1,2),则下一个有解区间为( )
| A. | (1,2) | B. | (1.75,2) | C. | (1.5,2) | D. | (1,1.5) |
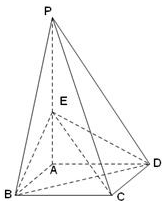 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.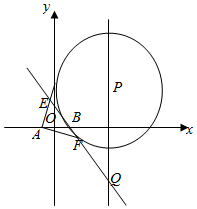 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.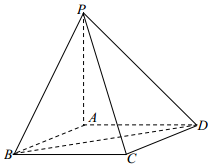 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PB=PC=PD.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PB=PC=PD.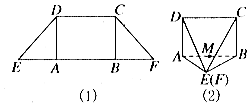 如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).
如图所示,在等腰梯形CDEF中,DE=CD=$\sqrt{2}$,EF=2+$\sqrt{2}$,将它沿着两条高AD,CB折叠成如图(2)所示的四棱锥E-ABCD(E,F重合).