题目内容
16.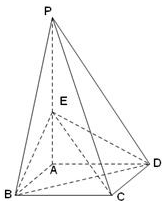 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.(1)求证:PC∥平面BDE
(2)求三棱锥P-CED的体积.
分析 (1)连结AC、BD,交于点O,连结OE,则OE∥PC,由此能证明PC∥平面BDE.
(2)三棱锥P-CED的体积VP-CED=VC-PDE,由此能求出结果.
解答 证明:(1) 连结AC、BD,交于点O,连结OE,
连结AC、BD,交于点O,连结OE,
∵四棱锥P-ABCD的底面是边长为1的正方形,
∴O是AC中点,
∵E是侧棱PA的中点,∴OE∥PC,
∵PC?平面BDE,OE?平面BDE,
∴PC∥平面BDE.
解:(2)∵四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点,
∴PA⊥CD,AD⊥CD,
∵PA∩AD=A,∴CD⊥平面PAD,
∵S△PDE=$\frac{1}{2}×AD×PE$=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
∴三棱锥P-CED的体积VP-CED=VC-PDE=$\frac{1}{3}×{S}_{△PDE}×CD$=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
4.已知三个数a=0.32,b=log20.3,c=20.3,则a,b,c之间的大小关系是( )
| A. | b<a<c | B. | a<b<c | C. | a<c<b | D. | b<c<a |
1.已知直线x=1上的点P到直线x-y=0的距离为$\sqrt{2}$,则点P的坐标为( )
| A. | (1,-1) | B. | (1,3) | C. | (1,-2)或(1,2) | D. | (1,-1)或(1,3) |
5.A是抛物线y2=2px(p>0)上的一点,F为抛物线的焦点,O为坐标原点,当|AF|=4时,∠OFA=120°,则抛物线的准线方程是( )
| A. | x=-1 | B. | y=-1 | C. | x=-2 | D. | y=-2 |
6.下列说法正确的是( )
| A. | “若a>1,则a2>1”的否命题是“若a>1,则a2≤1” | |
| B. | 在△ABC中,“A>B”是“sin2A>sin2B”必要不充分条件 | |
| C. | “若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 | |
| D. | ?x0∈(-∞,0)使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立 |