题目内容
求函数y=sin(x+
)+sinx的值域.
| π |
| 3 |
考点:两角和与差的正弦函数
专题:计算题,三角函数的图像与性质
分析:化简可得y=
sin(x+
),由sin(x+
)∈[-1,1],即可求得
sin(x+
)∈[-
,
].
| 3 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| π |
| 6 |
| 3 |
| 3 |
解答:
解:∵y=sin(x+
)+sinx=
sinx+
cosx+sinx=
sin(x+
)
∵sin(x+
)∈[-1,1]
∴
sin(x+
)∈[-
,
]
故函数y=sin(x+
)+sinx的值域为[-
,
].
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵sin(x+
| π |
| 6 |
∴
| 3 |
| π |
| 6 |
| 3 |
| 3 |
故函数y=sin(x+
| π |
| 3 |
| 3 |
| 3 |
点评:本题主要考查了两角和与差的正弦函数公式的应用,属于基本知识的考查.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
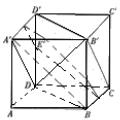 如图,ABCD-A1B1C1D1为正方体,任作平面a与对角线AC′垂直,使得a与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )
如图,ABCD-A1B1C1D1为正方体,任作平面a与对角线AC′垂直,使得a与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )| A、S为定值,l不为定值 |
| B、S不为定值,l为定值 |
| C、S与l均为定值 |
| D、S与l均不为定值 |
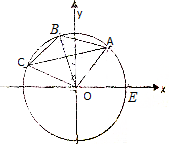 如图,已知单位圆上有四点E(1,0),A(cosθ,sinθ),B(cos2θ,sin2θ),C(cos3θ,sin3θ)(0<θ≤
如图,已知单位圆上有四点E(1,0),A(cosθ,sinθ),B(cos2θ,sin2θ),C(cos3θ,sin3θ)(0<θ≤