题目内容
若
≠0，
≠0，且|
|=|
|=|
-
|，则
与
+
所在直线的夹角是 ．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设
=
，
=
，则
-
=
．根据
≠0，
≠0，且|
|=|
|=|
-
|，可得△OAB是等边三角形．即可得出．
| OA |
| a |
| OB |
| b |
| a |
| b |
| BA |
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：设
=
，
=
，则
-
=
．
∵
≠0，
≠0，且|
|=|
|=|
-
|，
∴△OAB是等边三角形．
∴
与
+
所在直线的夹角是30°．
故答案为：30°．
| OA |
| a |
| OB |
| b |
| a |
| b |
| BA |
∵
| a |
| b |
| a |
| b |
| a |
| b |
∴△OAB是等边三角形．
∴
| a |
| a |
| b |
故答案为：30°．
点评：本题考查了向量的三角形法则、平行四边形法则，属于基础题．
练习册系列答案
相关题目
在四边形ABCD中，
=
+2
，
=-4
-
，
=-5
-3
，则四边形ABCD的形状是（ ）
| AB |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
| A、长方形 | B、平行四边形 |
| C、菱形 | D、梯形 |
过点P（3，2）与双曲线
-
=1有且只有一个公共点的直线有（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、一条 | B、二条 | C、三条 | D、四条 |
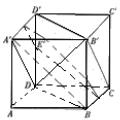如图，ABCD-A1B1C1D1为正方体，任作平面a与对角线AC′垂直，使得a与正方体的每个面都有公共点，记这样得到的截面多边形的面积为S，周长为l，则（ ）| A、S为定值，l不为定值 |
| B、S不为定值，l为定值 |
| C、S与l均为定值 |
| D、S与l均不为定值 |