题目内容
已知函数f(x)=x-1-lnx.
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)比较(1+
)(1+
)…(1+
)与e的大小(n∈N*,n>2,e是自然对数的底数);
(Ⅲ)对于函数h(x)和g(x)定义域上的任意实数x,若存在常数k,b,使得不等式h(x)≥kx+b和g(x)≤kx+b都成立,则称直线y=kx+b是函数h(x)和g(x)的“分界线”.设函数h(x)=
x2,g(x)=e[x-1-f(x)],试问函数h(x)和g(x)是否存在“分界线”?若存在,求出常数k,b的值.若不存在,说明理由.
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)比较(1+
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| n! |
(Ⅲ)对于函数h(x)和g(x)定义域上的任意实数x,若存在常数k,b,使得不等式h(x)≥kx+b和g(x)≤kx+b都成立,则称直线y=kx+b是函数h(x)和g(x)的“分界线”.设函数h(x)=
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:函数的性质及应用,导数的综合应用
分析:(Ⅰ)先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,通过列表求出极值及最小值即可;(Ⅱ)给(1+
)(1+
)…(1+
)和e取以e为底的对数,然后通过放缩不等式,使不等式变成已有的简单式子进行比较;(Ⅲ)令F(x)=h(x)-g(x),求导数F′(x),当当x∈(0,
)时,F′(x)<0,F(x)递减,当当x∈(
,+∞)时,F′(x)>0,F(x)递增,故当x=
时F(x)取得最小值0,则h(x)与g(x)的图象在x=
处有公共点(
,
),由此能够导出函数h(x)与g(x)存在“分界线”,其中k=
,b=-
.
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| n! |
| e |
| e |
| e |
| e |
| e |
| e |
| 2 |
| e |
| e |
| 2 |
解答:
解:(Ⅰ)∵f(x)=x-1-lnx,
∴f′(x)=1-
,
∴当x∈(0,1)时,f′(x)<0,f(x)是减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)是增函数;
∴f(x)在(0,+∞)上的极小值也为最小值,且最小值为f(1)=0;
(Ⅱ)据(Ⅰ)知f(x)=x-1-lnx≥0,知当x>0时,lnx≤x-1,
故当n>2时,ln[(1+
)(1+
)…(1+
)]=ln(1+
)+ln(1+
)+…+ln(1+
)≤(1+
-1)+(1+
-1)+…+(1+
-1)=
+
+…+
≤
+
+
+…+
=(1-
)+(
-
)(
-
)+…+(
-
)=1-
<1,
故(1+
)(1+
)…(1+
)<e;
(Ⅲ)令F(x)=h(x)-g(x)=
x2-e[x-1-(x-1-lnx)]=
x2-elnx(x>0),
则F′(x)=x-
=
(x>0),
∴当x∈(0,
)时,F′(x)<0,F(x)是减函数;
当x∈(
,+∞)时,F′(x)>0,F(x)是增函数;
∴F(x)的最小值F(
)=0,
则h(x)与g(x)的图象在x=
处有公共点(
,
),
设函数h(x)和g(x)存在“分界线”,方程为y-
=k(x-
),有h(x)≥kx+
-k
在x∈R时恒成立,即x2-2kx-e+2k
≥0在x∈R时恒成立,由△=4k2-4(2k
-e)=4(k-
)2≤0,得k=
,则“分界线”方程为y=
x-
;
记G(x)=elnx-
x+
(x>0),则G′(x)=
-
=
(x>0),
当x∈(0,
)时,G′(x)>0,函数G(x)是增函数;当x∈(
,+∞)时,G′(x)<0,函数G(x)是减函数.
∴当x=
时,函数G(x)取得最大值0,即g(x)≤
x-
在x>0时恒成立.
综上所述,函数h(x)和g(x)存在“分界线”,其中k=
,b=-
.
∴f′(x)=1-
| 1 |
| x |
∴当x∈(0,1)时,f′(x)<0,f(x)是减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)是增函数;
∴f(x)在(0,+∞)上的极小值也为最小值,且最小值为f(1)=0;
(Ⅱ)据(Ⅰ)知f(x)=x-1-lnx≥0,知当x>0时,lnx≤x-1,
故当n>2时,ln[(1+
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| n! |
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| n! |
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| n! |
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| n! |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n-1)×n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
故(1+
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| n! |
(Ⅲ)令F(x)=h(x)-g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
则F′(x)=x-
| e |
| x |
(x+
| ||||
| x |
∴当x∈(0,
| e |
当x∈(
| e |
∴F(x)的最小值F(
| e |
则h(x)与g(x)的图象在x=
| e |
| e |
| e |
| 2 |
设函数h(x)和g(x)存在“分界线”,方程为y-
| e |
| 2 |
| e |
| e |
| 2 |
| e |
| e |
| e |
| e |
| e |
| e |
| e |
| 2 |
记G(x)=elnx-
| e |
| e |
| 2 |
| e |
| x |
| e |
e-
| ||
| x |
当x∈(0,
| e |
| e |
∴当x=
| e |
| e |
| e |
| 2 |
综上所述,函数h(x)和g(x)存在“分界线”,其中k=
| e |
| e |
| 2 |
点评:本小题主要考查函数单调性的应用、利用导数求闭区间上函数的最值、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.

练习册系列答案
相关题目
过点P(3,2)与双曲线
-
=1有且只有一个公共点的直线有( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、一条 | B、二条 | C、三条 | D、四条 |
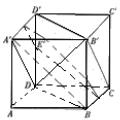 如图,ABCD-A1B1C1D1为正方体,任作平面a与对角线AC′垂直,使得a与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )
如图,ABCD-A1B1C1D1为正方体,任作平面a与对角线AC′垂直,使得a与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )| A、S为定值,l不为定值 |
| B、S不为定值,l为定值 |
| C、S与l均为定值 |
| D、S与l均不为定值 |
某化工产品受A、B、C三个因素的影响,每个因素有两个水平,分别用A1、A2,B1、B2,C1、C2表示.分析如下正交试验结果表,得到最佳因素组合(最佳因素组合是指实验结果最大的因素组合)为( )
| 实验号\列号 | A | B | C | 实验结果 |
| 1 | A1 | B1 | C1 | 79 |
| 2 | A1 | B2 | C2 | 65 |
| 3 | A2 | B1 | C2 | 88 |
| 4 | A2 | B2 | C1 | 81 |
| 1水平的平均值 | 72 | 83.5 | 80 | |
| 2水平的平均值 | 84.5 | 73 | 76.5 |
| A、(A1,B2,C1) |
| B、(A2,B1,C1) |
| C、(A2,B1,C2) |
| D、(A2,B2,C2) |
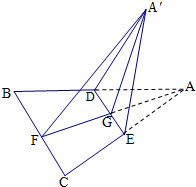 已知边长为a的正△ABC的中线AF与中位线DE相交于点G,现将△AED沿DE翻折为△A′ED,如图是翻折过程中的一个图形,则下列四个结论:
已知边长为a的正△ABC的中线AF与中位线DE相交于点G,现将△AED沿DE翻折为△A′ED,如图是翻折过程中的一个图形,则下列四个结论: