题目内容
已知f(x)的定义域为[0,1],则函数y=f(x2)及f(2x)+f(x+
)的定义域是 .
| 2 |
| 3 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由0≤x2≤1求解x的取值集合得y=f(x2)的定义域;
由
求解不等式组得x的取值集合得函数f(2x)+f(x+
)的定义域.
由
|
| 2 |
| 3 |
解答:
解:∵f(x)的定义域为[0,1],
由0≤x2≤1,得-1≤x≤1.
∴y=f(x2)的定义域为[-1,1];
由
,解得0≤x≤
.
∴函数f(2x)+f(x+
)的定义域为[0,
].
故答案为:[-1,1];[0,
].
由0≤x2≤1,得-1≤x≤1.
∴y=f(x2)的定义域为[-1,1];
由
|
| 1 |
| 3 |
∴函数f(2x)+f(x+
| 2 |
| 3 |
| 1 |
| 3 |
故答案为:[-1,1];[0,
| 1 |
| 3 |
点评:本题考查了函数的定义域及其求法,关键是掌握该类问题的求解方法,是基础题.

练习册系列答案
相关题目
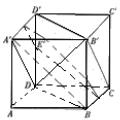 如图,ABCD-A1B1C1D1为正方体,任作平面a与对角线AC′垂直,使得a与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )
如图,ABCD-A1B1C1D1为正方体,任作平面a与对角线AC′垂直,使得a与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )| A、S为定值,l不为定值 |
| B、S不为定值,l为定值 |
| C、S与l均为定值 |
| D、S与l均不为定值 |
某化工产品受A、B、C三个因素的影响,每个因素有两个水平,分别用A1、A2,B1、B2,C1、C2表示.分析如下正交试验结果表,得到最佳因素组合(最佳因素组合是指实验结果最大的因素组合)为( )
| 实验号\列号 | A | B | C | 实验结果 |
| 1 | A1 | B1 | C1 | 79 |
| 2 | A1 | B2 | C2 | 65 |
| 3 | A2 | B1 | C2 | 88 |
| 4 | A2 | B2 | C1 | 81 |
| 1水平的平均值 | 72 | 83.5 | 80 | |
| 2水平的平均值 | 84.5 | 73 | 76.5 |
| A、(A1,B2,C1) |
| B、(A2,B1,C1) |
| C、(A2,B1,C2) |
| D、(A2,B2,C2) |