题目内容
已知F1、F2是椭圆C：
+
=1（a＞b＞0）的两个焦点，P为椭圆C上一点，且
⊥
．若△PF1F2的面积为16，则b= ．
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据椭圆的定义和勾股定理建立关于m、n的方程组，平方相减即可求出|PF1|•|PF2|=2b2，结合△PF1F2的面积为16，得到本题答案．
解答：
解：设|PF1|=m，|PF2|=n，
∵
⊥
，∴PF1⊥PF2，得∠F1PF2=90°，
∴m2+n2=4（a2-b2）
∵m+n=2a，（m+n）2=m2+n2+2mn，
∴mn=2b2，
∴|PF1|•|PF2|=2b2．
∴△PF1F2的面积S=
|PF1|•|PF2|=
×2b2=16，
∴b=4
故答案为：4．
∵
| PF1 |
| PF2 |
∴m2+n2=4（a2-b2）
∵m+n=2a，（m+n）2=m2+n2+2mn，
∴mn=2b2，
∴|PF1|•|PF2|=2b2．
∴△PF1F2的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
∴b=4
故答案为：4．
点评：本题给出椭圆的焦点三角形为直角三角形，求它的面积，着重考查了勾股定理、椭圆的定义和简单几何性质等知识．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
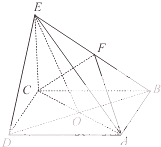在四棱锥E-ABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥底面ABCD，F为BE的中点．