题目内容
12.从1,2,3,4这四个数中一次随机取两个数,则两个数和为偶数的概率为$\frac{1}{3}$.分析 从1,2,3,4这四个数中一次随机取两个数,先求出基本事件总数,再求出两个数和为偶数包含怕基本事件个数,由此能求出这两个数和为偶数的概率.
解答 解:从1,2,3,4这四个数中一次随机取两个数,
基本事件总数n=${C}_{4}^{2}$=6,
两个数和为偶数包含怕基本事件个数m=${C}_{2}^{2}+{C}_{2}^{2}$=2,
∴这两个数和为偶数的概率p=$\frac{m}{n}$=$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{4x-4,x≤1}\\{{x}^{2}-4x+3,x>1}\end{array}\right.$,g(x)=lnx,则函数y=f(x)-g(x)的零点个数为( )
| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
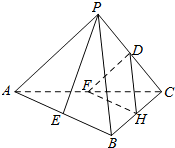 如图,在三棱锥P-ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.
如图,在三棱锥P-ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.