题目内容
已知四棱锥P-ABCD的底面为菱形,PD⊥底面ABCD.
(1)求证:△PAB≌△PCB;
(2)求证:AC⊥PB;
(3)若PD=2
,AB=
,二面角A-BP-C为120°,求四菱锥P-ABCD的体积.
(1)求证:△PAB≌△PCB;
(2)求证:AC⊥PB;
(3)若PD=2
| 2 |
| 5 |
考点:与二面角有关的立体几何综合题,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离,空间角
分析:(1)四棱锥P-ABCD的底面为菱形,PD⊥底面ABCD,可得PA=PC,AB=AC,即可证明:△PAB≌△PCB;
(2)证明:AC⊥平面PDB,即可证明AC⊥PB;
(3)若PD=2
,AB=
,二面角A-BP-C为120°,求出ABCD的面积,即可求出体积.
(2)证明:AC⊥平面PDB,即可证明AC⊥PB;
(3)若PD=2
| 2 |
| 5 |
解答:
(1)证明:∵四棱锥P-ABCD的底面为菱形,PD⊥底面ABCD,
∴PA=PC,AB=AC,
∵PB=PB,
∴△PAB≌△PCB;
(2)证明:∵四棱锥P-ABCD的底面为菱形,
∴AC⊥BD,
∴AC⊥PD,BD∩PD=D,
∴AC⊥平面PDB,
∵PB?平面PDB,
∴AC⊥PB;
(3)解:作AE⊥PB,连接CE,则CE⊥PB,
∴∠AEC=120°,
∵PD=2
,AB=
,
∴PA=
,PB=3
,
∴AE=
,
∴由余弦定理可得AC=
)=
,
∴cos∠ABC=
=-
,
∴sin∠ABC=
,
∴SABCD=
,
∴四棱锥P-ABCD的体积V=
•
•2
=
.
∴PA=PC,AB=AC,
∵PB=PB,
∴△PAB≌△PCB;
(2)证明:∵四棱锥P-ABCD的底面为菱形,
∴AC⊥BD,
∴AC⊥PD,BD∩PD=D,
∴AC⊥平面PDB,
∵PB?平面PDB,
∴AC⊥PB;
(3)解:作AE⊥PB,连接CE,则CE⊥PB,
∴∠AEC=120°,
∵PD=2
| 2 |
| 5 |
∴PA=
| 13 |
| 2 |
∴AE=
| ||
3
|
∴由余弦定理可得AC=
|
|
∴cos∠ABC=
5+5-
| ||||
2•
|
| 1 |
| 12 |
∴sin∠ABC=
| ||
| 12 |
∴SABCD=
5
| ||
| 12 |
∴四棱锥P-ABCD的体积V=
| 1 |
| 3 |
5
| ||
| 12 |
| 2 |
5
| ||
| 18 |
点评:本题考查三角形全等的证明,考查线面垂直,考查体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
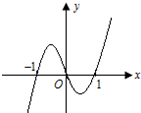 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )
已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )| A、f′(1)+f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf'(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
已知x、y满足约束条件
,则
的最小值为( )
|
| (x+1) 2+y 2 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|