题目内容

已知x、y满足约束条件
x≥0
y≥0
2x+y≥1
，则
(x+1) 2+y 2
的最小值为（　　）
A、
2
B、2
C、
3
5
5
D、
2
5
5
考点：简单线性规划
专题：计算题,作图题,不等式的解法及应用
分析：作出平面区域，（x+1）2+y2的几何意义解答．
解答： 解：其平面区域如图：
(x+1) 2+y 2
的几何意义为阴影部分内的点到点A（-1，0）的距离，
则
(x+1) 2+y 2
的最小值为以点A为圆心的圆与直线2x+y=1相切时的半径，
即点A到直线2x+y=1的距离．
点A到直线2x+y=1的距离d=
|2×(-1)-1|
22+1
=
3
5
=
3
5
5
，
故选C．
点评：本题考查了线性规划，作图要细致，注意联系其几何意义．属于中档题．
练习册系列答案
相关题目
已知四棱锥P-ABCD的底面为菱形，PD⊥底面ABCD．
（1）求证：△PAB≌△PCB；
（2）求证：AC⊥PB；
（3）若PD=2
2
，AB=
5
，二面角A-BP-C为120°，求四菱锥P-ABCD的体积．
已知y=f（x）是定义在[-1，1]上的奇函数，x∈[0，1]时，f（x）=
4x+a
4x+1
．
（1）求x∈[-1，0）时，y=f（x）解析式；
（2）解不等式f（x）＞
1
5
．
已知幂函数f（x）=x 
3
2
+k-
1
2
k2（k∈z）为偶函数，且在区间（0，+∞）上为增函数，求f（x）的解析式．
已知定义在R上的偶函数f（x），当x≥0时，f（x）=x|x-2|．
（1）求y=f（x）的解析式．
（2）若函数y=a与函数y=f（x）有6个交点，求a的取值范围．
对于有理数a，b（a+b≠0）定义运算“*”如下：a*b=
ab
a+b
，求2*3和（-3）*（-4）的值．
函数f（x）=（m-4）x3+10x在[1，2]上最大值为4，则实数m=
 
．
已知切线C的极坐标方程是ρ=2，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线L的参数方程为
x=1-
1
2
t
y=2+
3
2
t
（t为参数）．
（1）写出直线L与曲线C的直角坐标系下的方程；
（2）设曲线C经过伸缩变换
x′=x
y′=2y
，得到曲线C′，判断L与切线C′交点的个数．
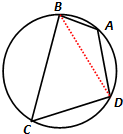已知圆内接四边形ABCD的边AB=1，BC=3，CD=DA=2．
（Ⅰ）求角C的大小和BD的长；
（Ⅱ）求四边形ABCD的面积及外接圆半径．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网