题目内容
若函数f(x)=|ax+x2-xlna-t|-1(a>1)有三个零点,则t的值是( )
| A、2 | B、4 | C、8 | D、0 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数f(x)=|g(x)-t|-1有三个零点,转化为g(x)=t±1共有三个根,即y=g(x)的图象与两条平行于x轴的直线y=t±1共有三个交点,根据t-1<t+1,
可得g(x)=t+1有两个根,g(x)=t-1只有一个根,从而可求t的值.
可得g(x)=t+1有两个根,g(x)=t-1只有一个根,从而可求t的值.
解答:
解:令g(x)=)=ax+x2-xlna,(a>1).
g′(x)=2x+(ax-1)lna=0,得到x=0,g(x),g′(x)的变化情况如下表:
因为函数f(x)=|g(x)-t|-1有三个零点,所以g(x)=t±1共有三个根,即y=g(x)的图象与两个平行于x轴的直线y=t±1共有三个交点.
y=g(x)在(-∞,0)递减,在(0,+∞)递增,极小值f(0)=1也是最小值,当x→±∞时,f(x)→+∞.
∵t-1<t+1,∴f(x)=t+1有两个根,f(x)=t-1只有一个根.
∴t-1=fmin(x)=f(0)=1,∴t=2.
故选:A.
g′(x)=2x+(ax-1)lna=0,得到x=0,g(x),g′(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,+∞) |
| g′(x) | - | 0 | + |
| g(x) | 递减 | 极小值1 | 递增 |
y=g(x)在(-∞,0)递减,在(0,+∞)递增,极小值f(0)=1也是最小值,当x→±∞时,f(x)→+∞.
∵t-1<t+1,∴f(x)=t+1有两个根,f(x)=t-1只有一个根.
∴t-1=fmin(x)=f(0)=1,∴t=2.
故选:A.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的零点,考查学生分析解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,设点P(x,y),定义[OP]=|x|+|y|,其中O为坐标原点.对于下列结论:
(1)符合[OP]=1的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:
x+2y-2=0上任意一点,则[OP]min=1;
(3)设点P是直线:y=kx+1(k∈R)上任意一点,则“使得[OP]最小的点P有无数个”的充要条件是“k=±1”;
(4)设点P是圆x2+y2=1上任意一点,则[OP]max=
.
其中正确的结论序号为( )
(1)符合[OP]=1的点P的轨迹围成的图形的面积为2;
(2)设点P是直线:
| 5 |
(3)设点P是直线:y=kx+1(k∈R)上任意一点,则“使得[OP]最小的点P有无数个”的充要条件是“k=±1”;
(4)设点P是圆x2+y2=1上任意一点,则[OP]max=
| 2 |
其中正确的结论序号为( )
| A、(1)、(2)、(3) |
| B、(1)、(3)、(4) |
| C、(2)、(3)、(4) |
| D、(1)、(2)、(4) |
某几何体的三视图如图所示,它的体积为( )
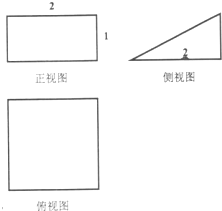

| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
 如图,有一块边长为1km的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45° (其中点P,Q分别在边BC,CD上),设∠PAB=θ,tanθ=t
如图,有一块边长为1km的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45° (其中点P,Q分别在边BC,CD上),设∠PAB=θ,tanθ=t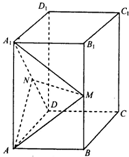 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.