题目内容

曲线y=-3x3+2在点（0，2）处的切线的斜率是（　　）
A、-6B、6C、0D、不存在
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：由已知函数求其导函数，在导函数解析式中取x=0得答案．
解答： 解：∵y=-3x3+2，∴y′=-9x2，
则y′|x=0=0，
即曲线y=-3x3+2在点（0，2）处的切线的斜率是0．
故选：C．
点评：本题考查了利用导数研究过曲线上某点处的切线方程，过曲线上某点的切线的斜率，就是函数在该点处的导数值，是基础题．
练习册系列答案
相关题目
巳知向量
m
=（
3
sin
x
4
，1），
n
=（cos
x
4
，cos2
x
4
），f（x）=
m
•
n

（Ⅰ）若f（x）=1，求cos（
π
3
+x）的值；
（Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a-c）cosB=bcosC，求函数f（A）的取值范围．
某几何体的三视图如图所示，它的体积为（　　）
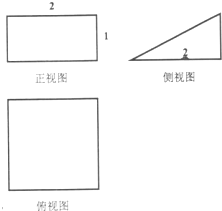
A、2
B、4
C、
2
3
D、
4
3
函数y=cos2ax-sin2ax的最小正周期为π，则a的值是（　　）
A、-1B、1C、2D、±1
从10名女生和5名男生中选出6名组成课外学习小组，则选出4女2男组成课外学习小组的概率是
 
．（精确到0.01）
已知点M（x，y）在不等式组
x-y+5≥0
x+y≤0
y≥0
所表示的平面区域内，则z=（x-1）2+（y-2）2的最小值为
 
．
求导f（x）=
1+
x
1-
x
+
1-
x
1+
x
．
已知复数z=
1+2i
3-i
，i是虚数单位，则复数z的虚部是（　　）
A、
1
10
i
B、
1
10
C、
7
10
i
D、
7
10
若方程
x2
2-k
+
y2
k-1
=1表示图形分别是①双曲线，②圆，③椭圆，则k的取值范围分别为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网