题目内容
若关于x的不等式ax2+7x+4>0的解集是{x|-
<x<4}.
(1)求关于x的不等式 ma•x2+(m+a)x+3+a>0(m≥0)的解集;
(2)若关于x的不等式 ma•x2+(m+a)x+3+a>0恒成立,求实数m的取值范围.
| 1 |
| 2 |
(1)求关于x的不等式 ma•x2+(m+a)x+3+a>0(m≥0)的解集;
(2)若关于x的不等式 ma•x2+(m+a)x+3+a>0恒成立,求实数m的取值范围.
考点:一元二次不等式的解法,函数恒成立问题
专题:不等式的解法及应用
分析:(1)关于x的不等式ax2+7x+4>0的解集是{x|-
<x<4},可知:-
,4是一元二次方程ax2+7x+4=0的两个实数根,利用根与系数的关系即可得出a.再对a分类讨论利用一元二次不等式的解法即可得出.
(2)关于x的不等式 ma•x2+(m+a)x+3+a>0恒成立,由(1)化为2mx2+(2-m)x-1<0.当m=0时,即可知道不满足条件;当m≠0时,不等式恒成立,则△<0,解出即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)关于x的不等式 ma•x2+(m+a)x+3+a>0恒成立,由(1)化为2mx2+(2-m)x-1<0.当m=0时,即可知道不满足条件;当m≠0时,不等式恒成立,则△<0,解出即可.
解答:
解:(1)∵关于x的不等式ax2+7x+4>0的解集是{x|-
<x<4},
∴-
,4是一元二次方程ax2+7x+4=0的两个实数根,
∴-
×4=
,解得a=-2.
不等式 ma•x2+(m+a)x+3+a>0(m≥0)即为-2mx2+(m-2)x+1>0,化为2mx2+(2-m)x-1<0.
当m=0时,不等式化为2x-1<0,解得x<
;
当m>0时,不等式化为(mx+1)(2x-1)<0,解得-
<x<
.
∴当m=0时,不等式的解集为{x|x<
};
当m>0时,不等式的解集为{x|-
<x<
}.
(2)关于x的不等式 ma•x2+(m+a)x+3+a>0恒成立,由(1)化为2mx2+(2-m)x-1<0.
可得:当m=0时,不等式的解集为{x|x<
},不满足条件;
当m≠0时,不等式恒成立,
则△=(2-m)2+8m<0,化为(2+m)2<0,解集为∅,
因此实数m的取值范围是∅.
| 1 |
| 2 |
∴-
| 1 |
| 2 |
∴-
| 1 |
| 2 |
| 4 |
| a |
不等式 ma•x2+(m+a)x+3+a>0(m≥0)即为-2mx2+(m-2)x+1>0,化为2mx2+(2-m)x-1<0.
当m=0时,不等式化为2x-1<0,解得x<
| 1 |
| 2 |
当m>0时,不等式化为(mx+1)(2x-1)<0,解得-
| 1 |
| m |
| 1 |
| 2 |
∴当m=0时,不等式的解集为{x|x<
| 1 |
| 2 |
当m>0时,不等式的解集为{x|-
| 1 |
| m |
| 1 |
| 2 |
(2)关于x的不等式 ma•x2+(m+a)x+3+a>0恒成立,由(1)化为2mx2+(2-m)x-1<0.
可得:当m=0时,不等式的解集为{x|x<
| 1 |
| 2 |
当m≠0时,不等式恒成立,
则△=(2-m)2+8m<0,化为(2+m)2<0,解集为∅,
因此实数m的取值范围是∅.
点评:本题考查了一元二次不等式的解法、分类讨论的思想方法、一元二次方程的根与系数的关系等基础知识与基本技能方法,考查了推理能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
三人相互传球,由甲开始发球,经过5次传球后,球仍回到甲手中,则不同的传球方法的种数是( )
| A、6 | B、8 | C、10 | D、16 |
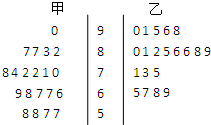 为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.