题目内容
设函数f(x)=ax-a-x(a>0且a≠1).
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)若0<a<1,解不等式f(x2+6x)+f(4-x)<0;
(3)若f(1)=
,g(x)=a2x+a-2x-2mf(x)且g(x)在[1,+∞)上的最小值为-2,求m的值.
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)若0<a<1,解不等式f(x2+6x)+f(4-x)<0;
(3)若f(1)=
| 3 |
| 2 |
考点:函数单调性的性质,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)根据函数f(x)的定义域为R,关于原点对称,且f(-x)-f(x),可得f(x)为奇函数.
(2)0<a<1,不等式即 f(x2+6x)<f(x-4),根据f(x)=ax-a-x 在R上单调递减,可得x2+6x>x-4,由此求得不等式的解集.
(3)由f(1)=
,求得得a=2,令t=2x-2-x,由f(x)=2x-2-x为增函数,x≥1,可得t≥f(1)=
,令g(x)=h(t)=t2-2mt+2,利用二次函数的性质,分类讨论求得h(t)的最小值.
(2)0<a<1,不等式即 f(x2+6x)<f(x-4),根据f(x)=ax-a-x 在R上单调递减,可得x2+6x>x-4,由此求得不等式的解集.
(3)由f(1)=
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)函数f(x)=ax-a-x(a>0且a≠1)的定义域为R,关于原点对称,
且f(-x)=a-x-ax=-f(x),a>0且a≠1),故f(x)为奇函数.
(2)0<a<1,解不等式f(x2+6x)+f(4-x)<0,即 f(x2+6x)<f(x-4)
又f(x)=ax-a-x 在R上单调递减,∴x2+6x>x-4,解得 x<-4,或x>-1,
故不等式的解集为{x|x<-4,或x>-1}.
(3)∵f(1)=
,∴a-
=
,解得a=2,或a=-
(舍去),
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=2x-2-x,则g(x)=t2-2mt+2,由(1)可知f(x)=2x-2-x为增函数.
∵x≥1,∴t≥f(1)=
,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥
),
若m≥
,当t=m时,h(t)min=2-m2=-2,∴m=2;
若m<
,当t=
时,h(t)min=
-3m=-2,解得m=
>
,(舍去)
综上可知m=2.
且f(-x)=a-x-ax=-f(x),a>0且a≠1),故f(x)为奇函数.
(2)0<a<1,解不等式f(x2+6x)+f(4-x)<0,即 f(x2+6x)<f(x-4)
又f(x)=ax-a-x 在R上单调递减,∴x2+6x>x-4,解得 x<-4,或x>-1,
故不等式的解集为{x|x<-4,或x>-1}.
(3)∵f(1)=
| 3 |
| 2 |
| 1 |
| a |
| 3 |
| 2 |
| 1 |
| 2 |
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=2x-2-x,则g(x)=t2-2mt+2,由(1)可知f(x)=2x-2-x为增函数.
∵x≥1,∴t≥f(1)=
| 3 |
| 2 |
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥
| 3 |
| 2 |
若m≥
| 3 |
| 2 |
若m<
| 3 |
| 2 |
| 3 |
| 2 |
| 17 |
| 4 |
| 25 |
| 12 |
| 3 |
| 2 |
综上可知m=2.
点评:本题主要考查求函数的定义域,函数的单调性的应用,利用二次函数的性质求函数的最值,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知i是虚数单位,复数
的模为( )
| -5+i |
| 2-3i |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
已知函数f(x)对任意的实数x,都有f(2+x)=f(2-x),f(1+x)=-f(x),且f(x)不恒为0,则f(x)是( )
| A、奇函数但非偶函数 |
| B、偶函数但非奇函数 |
| C、既是奇函数又是偶函数 |
| D、是非奇非偶函数 |
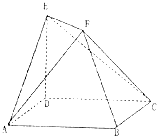 如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD.
如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF∥BD,且2EF=BD.