题目内容
已知a∈(0,
),b∈[0,
],则2a-
的范围 .
| π |
| 2 |
| π |
| 2 |
| b |
| 3 |
考点:不等关系与不等式
专题:计算题,不等式的解法及应用
分析:由题意,由a、b的范围先求2a,
的范围,从而求2a-
的取值范围.
| b |
| 3 |
| b |
| 3 |
解答:
解:∵a∈(0,
),b∈[0,
],
∴2a∈(0,π),
∈[0,
],
∴-
<2a-
<π,
故答案为:(-
,π).
| π |
| 2 |
| π |
| 2 |
∴2a∈(0,π),
| b |
| 3 |
| π |
| 6 |
∴-
| π |
| 6 |
| b |
| 3 |
故答案为:(-
| π |
| 6 |
点评:本题考查了不等式的性质应用,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
已知在等比数列{an}中,a1=
,公比q=
.
(1)Sn为{an}的前n项和,证明:Sn=
;
(2)设bn=log
a1+log
a2+…+log
an,求数列{bn}的通项公式.
| 1 |
| 3 |
| 1 |
| 3 |
(1)Sn为{an}的前n项和,证明:Sn=
| 1-an |
| 2 |
(2)设bn=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
已知F1、F2分别是椭圆M:
+
=1(a>
)的左右焦点,点P是椭圆M上一点,且
•
=0,则离心率e取最小值时椭圆M的方程为( )
| x2 |
| a2 |
| y2 |
| a2-2 |
| 2 |
| PF1 |
| PF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
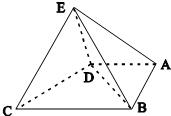 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.