题目内容
1.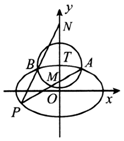 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.(Ⅰ)求椭圆C的方程;
(Ⅱ)求$\overrightarrow{TA}•\overrightarrow{TB}$的最小值,并求出此时圆T的方程;
(Ⅲ)设点P是椭圆C上异于A,B的一点,且直线PA,PB分别与Y轴交于点M,N,O为坐标原点,求证:|OM|•|ON|为定值.
分析 (Ⅰ)求出b的值,根据e=$\frac{c}{a}$,从而求出椭圆的方程即可;
(Ⅱ)设出A(x1,y1),B(-x1,y1),求出$\overrightarrow{TA}$•$\overrightarrow{TB}$的表达式,根据二次函数的性质求出其最小值,从而求出A的坐标即可;
(Ⅲ)设p(x0,y0),则PA的方程为y-y0=$\frac{{{y}_{0}-y}_{1}}{{{x}_{0}-x}_{1}}$(x-x0),分别求出yM和yN的值,从而证出|OM|•|ON|为定值.
解答 解:(Ⅰ)由椭圆得:b=1,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∴a2-c2=1,$\frac{{c}^{2}}{{a}^{2}}$=$\frac{3}{4}$,得a2=4,c2=3,b2=1,
故椭圆C的方程为$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)∵点A与点B关于y轴对称,
设A(x1,y1),B(-x1,y1),
由点A在椭圆C上,则${{x}_{1}}^{2}$=4-4${{y}_{1}}^{2}$,
∵T(0,1),得$\overrightarrow{TA}$=(x1,y1-1),$\overrightarrow{TB}$=(-x1,y1-1),
∴$\overrightarrow{TA}$•$\overrightarrow{TB}$=-${{x}_{1}}^{2}$+${{(y}_{1}-1)}^{2}$=4${{y}_{1}}^{2}$-4+${{y}_{1}}^{2}$-2y1+1=5${{(y}_{1}-\frac{1}{5})}^{2}$-$\frac{16}{5}$,
由题意得,0<y1<1,
∴当y1=$\frac{1}{5}$时,$\overrightarrow{TA}$•$\overrightarrow{TB}$取得最小值-$\frac{16}{5}$,
此时,${{x}_{1}}^{2}$=4-$\frac{4}{25}$,x1=$\frac{4\sqrt{6}}{5}$,
故A($\frac{4\sqrt{6}}{5}$,$\frac{1}{5}$),
又点A在圆T上,带入圆的方程,得r2=$\frac{112}{25}$,
故圆T的方程是x2+(y-1)2=$\frac{112}{25}$;
(Ⅲ)设p(x0,y0),则PA的方程为y-y0=$\frac{{{y}_{0}-y}_{1}}{{{x}_{0}-x}_{1}}$(x-x0),
令x=0,得yM=y0-$\frac{({{y}_{0}-y}_{1}{)x}_{0}}{{{x}_{0}-x}_{1}}$=$\frac{{{{{x}_{0}y}_{1}-x}_{1}y}_{0}}{{{x}_{0}-x}_{1}}$,
同理可得,yN=$\frac{{{x}_{0}y}_{1}{{+x}_{1}y}_{0}}{{{x}_{0}+x}_{1}}$,
故yM•yN=$\frac{{{{{x}_{0}}^{2}y}_{1}}^{2}{{{{-x}_{1}}^{2}y}_{0}}^{2}}{{{{{x}_{0}}^{2}-x}_{1}}^{2}}$①,
∵p(x0,y0),A(x1,y1)都在椭圆C上,
∴${{y}_{0}}^{2}$=1-$\frac{{{x}_{0}}^{2}}{4}$,${{y}_{1}}^{2}$=1-$\frac{{{x}_{1}}^{2}}{4}$,
带入①得,yM•yN=$\frac{{{x}_{0}}^{2}(1-\frac{{{x}_{1}}^{2}}{4}){{-x}_{1}}^{2}(1-\frac{{{x}_{0}}^{2}}{4})}{{{{{x}_{0}}^{2}-x}_{1}}^{2}}$=1,
即得|OM|•|ON|=|yM•yN|=1为定值.
点评 本题考查了椭圆的性质,考查斜率问题以及二次函数的性质,考查计算能力,是一道综合题.

 习题精选系列答案
习题精选系列答案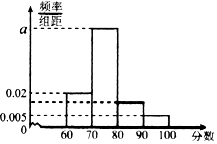 某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [60,70) | 16 | 0.2 |
| [70,80) | 50 | n |
| [80,90) | 10 | P |
| [90,100] | 4 | 0.05 |
| 合计 | M | I |
(II)如果用分层抽样的方法,从样本成绩在[60,70]和[90,100]的学生中共抽取5人,再从5人中选2人,求这2人成绩在[60,70]的概率.
| A. | b>c>a | B. | c>b>a | C. | b>a>c | D. | a>b>c |