题目内容

设x，y，z∈R，且满足x2+y2+z2=5，则x+2y+3z之最大值为
 
．
考点：二维形式的柯西不等式
专题：不等式的解法及应用
分析：由条件利用柯西不等式可得 14（x2+y2+z2）≥（x+2y+3z）2，由此求得x+2y+3z之最大值．
解答： 解：∵x2+y2+z2=5，12+22+32=14，利用柯西不等式可得 14（x2+y2+z2）≥（x+2y+3z）2，
即14×5）≥（x+2y+3z）2，∴x+2y+3z≤
70
，当且仅当
x
1
=
y
2
=
z
3
时，取等号，
故x+2y+3z之最大值为
70
，
故答案为：
70
．
点评：本题主要考查柯西不等式的应用，属于基础题．
练习册系列答案
相关题目
已知
a
=（
3
sinx，m+cosx），
b
=（cosx，-m+cosx），且f（x）=
a
•
b

（1）求函数f（x）的最小正周期
（2）当x∈[-
π
6
，
π
3
]时，f（x）的最小值是-4，求此时m的值和函数f（x）的最大值，并求出相应的x的值．
求证：|x+
1
x
|≥2．
已知函数f（x）=sinxcosx-
3
cos（π+x）cosx（x∈R）．则f（x）的最大值=
 
．
函数y=
-x2+3x-2
的定义域是
 
．
若关于x的不等式sin2x-（a+1）sinx+1≥0对一切x∈[0，
π
2
]恒成立，则a∈
 
．
已知平面直角坐标系xoy上的区域D由不等式组
x+y≥2
x＜2
y≤1
给定，若M（x，y）为D上的动点，则
9x2+y2
xy
的取值范围是
 
．
已知命题p：“?x∈[1，2]，x2-a≥0“，命题q：“?x0∈R，x02+2ax0+2=0“，若命题“p且q“是真命题，则实数a的取值范围是
 
．
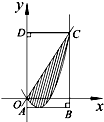如图，矩形ABCD内的阴影部分是由曲线f（x）=2x2-2x及直线y=2x围成的，现向矩形ABCD内随机投掷一点，则该点落在阴影部分的概率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网