题目内容
18.已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式f(x-1)+f(3-2x)≤0的解集.
分析 (1)由题意可知$\left\{\begin{array}{l}-2<x-1<2\\-2<3-2x<2\end{array}\right.$,即可求函数g(x)的定义域;
(2)不等式f(x-1)+f(3-2x)≤0转化为f(x-1)≤f(2x-3),利用f(x)在(-2,2)上单调递减,即可得出结论.
解答 解 (1)由题意可知$\left\{\begin{array}{l}-2<x-1<2\\-2<3-2x<2\end{array}\right.$(3分)
∴$\left\{\begin{array}{l}-1<x<3\\ \frac{1}{2}<x<\frac{5}{2}\end{array}\right.$,解得$\frac{1}{2}<x<\frac{5}{2}$. (5分)
故函数g(x)的定义域为($\frac{1}{2}$,$\frac{5}{2}$). (6分)
(2)由g(x)≤0,得f(x-1)+f(3-2x)≤0,
∴f(x-1)≤-f(3-2x).
∵f(x)为奇函数,
∴f(x-1)≤f(2x-3). (8分)
而f(x)在(-2,2)上单调递减,
∴$\left\{\begin{array}{l}x-1≥2x-3\\ \frac{1}{2}<x<\frac{5}{2}\end{array}\right.$解得$\frac{1}{2}<x≤2$. (11分)
∴g(x)≤0的解集为($\frac{1}{2}$,2].(12分)
点评 本题考查求函数g(x)的定义域,考查函数的单调性与奇偶性的结合,考查学生分析解决问题的能力,属于中档题.

| A. | ($\frac{1}{e}$,1) | B. | ($\frac{e}{e-1}$,e) | C. | ($\frac{1}{e}$,e) | D. | (1,e) |
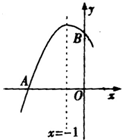 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论: