题目内容
17.设周期函数f(x)是定义在R上的奇函数,若f(x)的最小正周期为3,且满足f(1)>-2,f(2)=m2-m,则m的取值范围是(-1,2).分析 根据f(x)为奇函数且周期为3便可得到f(2)=-f(1),这便得到f(1)=-m2+m,根据f(1)>-2即可得到-m2+m>-2,解该不等式即可得到m的取值范围.
解答 解:根据条件得:f(2)=f(2-3)=f(-1)=-f(1)=m2-m;
∴f(1)=-m2+m;
∵f(1)>-2;
∴-m2+m>-2;
解得-1<m<2;
∴m的取值范围为(-1,2).
故答案为:(-1,2).
点评 考查奇函数和周期函数的定义,最小正周期的概念,以及解一元二次不等式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
7.如某校高中三年级的300名学生已经编号为0,1,…,299,为了了解学生的学习情况,要抽取一个样本数为60的样本,用系统抽样的方法进行抽取,若第60段所抽到的编号为298,则第1段抽到的编号为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.下列变量是线性相关的是( )
| A. | 人的身高与视力 | B. | 角的大小与弧长 | ||
| C. | 收入水平与消费水平 | D. | 人的年龄与身高 |
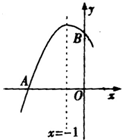 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论: