若复数z满足(3-z)•i=2.则z=3+2i．题目和参考答案——青夏教育精英家教网——

题目内容

19．若复数z满足（3-z）•i=2（i为虚数单位），则z=3+2i．

分析设出z=a+bi，根据系数对应相等，求出a，b的值即可．

解答解：设z=a+bi，
则（3-a-bi）i=b+（3-a）i=2，
故b=2，a=3，
故z=3+2i，
故答案为：3+2i．

点评本题考查了复数的定义及其运算性质，是一道基础题．

练习册系列答案

名校金典课堂系列答案

指南针高分必备系列答案

育才金典系列答案

智慧树同步讲练测系列答案

小学互动课堂同步训练系列答案

期末精华系列答案

轻松夺冠轻松课堂系列答案

顶尖课课练系列答案

快乐练练吧青海人民出版社系列答案

优质课堂系列答案

相关题目

9．凸四边形OABC中，$\overrightarrow{OB}=（2，4），\overrightarrow{AC}$=（-2，1），则该四边形的面积为（　　）

10．已知p：函数f（x）=（x-a）²在（-∞，-1）上是减函数，$q：?x＞0，a≤\frac{{{x^2}+1}}{x}$恒成立，则￢p是q的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

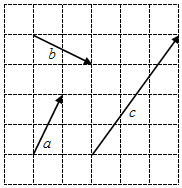如图，网格纸上小正方形的边长为1，若起点和终点均在格点的向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R），则x+y=$\frac{13}{5}$．

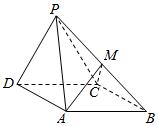如图，四棱锥P-ABCD中，底面ABCD是菱形，∠ADC=60°，面PCD⊥面ABCD，PC=PD=CD=2，点M为线段PB上异于P、B的点．
（Ⅰ）当点M为PB的中点时，求证：PD∥平面ACM
（Ⅱ）当二面角B-AC-M的余弦值为$\frac{\sqrt{5}}{5}$时，试确定点M的位置．

4．已知i为虚数单位，复数z=1+2i，z与$\overline z$共轭，则$z\overline z$等于（　　）

11．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$，A为左顶点，B为短轴端点，F为右焦点，且AB⊥BF，则椭圆的离心率为（　　）

$\frac{{\sqrt{5}+1}}{2}$

$\frac{{\sqrt{5}-1}}{2}$

$\frac{{\sqrt{3}+1}}{2}$

$\frac{{\sqrt{3}-1}}{2}$

8．根据下面程序框图，当n=2时，输出S=（　　）

9．设复数z满足z•（2+i）=10-5i（i为虚数单位），则z的共轭复数$\overline{z}$为（　　）