题目内容

15．设等比数列{an}的前n项和为Sn，若a2013=2S2014+6，3a2014=2S2015+6，则数列{an}的公比q等于1或$\frac{1}{2}$．

分析 已知两式相减结合等比数列的通项公式和求和公式可得q的方程，解方程可得．

解答 解：由题意可知a2013=2S2014+6，①
3a2014=2S2015+6a2013=2S2014+6，②
②-①可得3a2014-a2013=2S2015-2S2014=2a2015，
∴3a2013q-a2013=2a2013q2，
∴2q2-3q+1=0，
解得q=1或q=$\frac{1}{2}$．
故答案为：1或$\frac{1}{2}$．

点评 本题考查等比数列的求和公式，涉及通项公式和一元二次方程，属中档题．

练习册系列答案
相关题目
5．在△ABC中，b2=ac，cosB=$\frac{3}{4}$．
（1）求cotA+cotC的值；
（2）设△ABC的面积为sinB，求a+c的值．
6．在△ABC，角A，B，C所对的边分别为a，b，c，面积为S．已知a2-（b-c）2=$\frac{4}{3}$S
（1）求sinA的值；
（2）设M=2sin2B-$\frac{5}{7}$cos（B-C），求M的最大值．
3．已知sin（$\frac{5}{6}$π-α）=a，则sin（α+$\frac{7}{6}$π）=-a．
10．在数列{an}中，an+1=3an+3n，a1=1，求{an}的通项公式．
2．已知矩形ABCD中，AB=2AD=2，O为CD的中点，沿AO将三角形AOD折起，使DB=$\sqrt{3}$，如图所示，H为AO的中点．
（1）求证：平面AOD⊥平面ABCO；
（2）求二面角O-DB-H的余弦值．
9．凸四边形OABC中，$\overrightarrow{OB}=（2，4），\overrightarrow{AC}$=（-2，1），则该四边形的面积为（　　）
A．$\sqrt{5}$B．$2\sqrt{5}$C．5D．10
6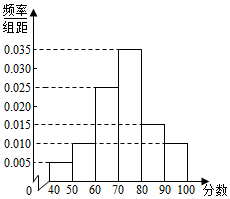．某中学对1000名学生的英语拓展水平测试成绩进行统计，得到样本频率分布直方图如图所示，现规定不低于80分为优秀，则优秀人数是（　　）
A．250B．200C．150D．100
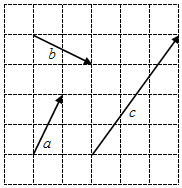7．如图，网格纸上小正方形的边长为1，若起点和终点均在格点的向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R），则x+y=$\frac{13}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网