题目内容
17.已知函数f(x)=a|x|-3a-1,若命题?x∈[-1,1],使f(x)≠0是假命题,则实数a的取值范围为( )| A. | $(-∞,\;-\frac{1}{2}]$ | B. | $(-∞,\;-\frac{1}{2}]∪(0,\;+∞)$ | C. | $[-\frac{1}{2},\;-\frac{1}{3}]$ | D. | $(-∞,\;-\frac{1}{3}]∪$$[-\frac{1}{2},\;0)$ |
分析 函数f(x)是偶函数,因此只考虑x∈[0,1]时,使f(x)≠0是假命题,因此存在x∈[0,1]时,使得f(x)=0是真命题.可得f(0)f(1)≤0,解出即可得出.
解答 解:∵函数f(x)是偶函数,因此只考虑x∈[0,1]时,使f(x)≠0是假命题,因此存在x∈[0,1]时,使得f(x)=0是真命题.
∴f(0)f(1)≤0,
解得$-\frac{1}{2}≤a≤-\frac{1}{3}$.
故选:C.
点评 本题考查了函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.根据下面程序框图,当n=2时,输出S=( )


| A. | 1000 | B. | 1950 | C. | 2850 | D. | 3800 |
5.已知i为虚数单位,a为正实数,若|$\frac{a-i}{i}$|=2,则a=( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
9.设复数z满足z•(2+i)=10-5i(i为虚数单位),则z的共轭复数$\overline{z}$为( )
| A. | -3+4i | B. | -3-4i | C. | 3+4i | D. | 3-4i |
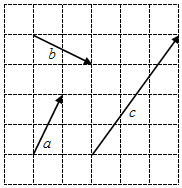 如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.
如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.