题目内容
12.在平行四边形ABCD中,$AB=\frac{1}{2},∠BAD=\frac{π}{3},E$为CD的中点,若$\overrightarrow{AC}•\overrightarrow{BE}=1$.则AD的长为1.分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AC},\overrightarrow{BE}$,代入数量积公式解出AD.
解答 解:$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,$\overrightarrow{BE}$=$\overrightarrow{BC}+\overrightarrow{CE}$=-$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{AD}$.
∴$\overrightarrow{AC}•\overrightarrow{BE}$=($\overrightarrow{AB}+\overrightarrow{AD}$)•(-$\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}$)=-$\frac{1}{2}{\overrightarrow{AB}}^{2}$+$\frac{1}{2}\overrightarrow{AB}•\overrightarrow{AD}$+${\overrightarrow{AD}}^{2}$=1.
∵$\overrightarrow{AB}•\overrightarrow{AD}$=$\frac{AD}{4}$,${\overrightarrow{AD}}^{2}$=AD2,${\overrightarrow{AB}}^{2}=\frac{1}{4}$.
∴AD2+$\frac{1}{8}AD$-$\frac{1}{8}$=1,解得AD=1.
故答案为:1.
点评 本题考查了平面向量线性运算,数量积运算,属于中档题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案| A. | -$\frac{7}{8}$ | B. | -$\frac{\sqrt{15}}{8}$ | C. | 1 | D. | $\frac{\sqrt{15}}{8}$ |
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 5 |
 已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=$\sqrt{3}$,如图所示,H为AO的中点.
已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=$\sqrt{3}$,如图所示,H为AO的中点.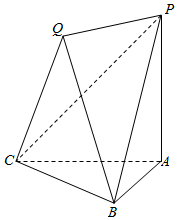 如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.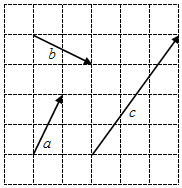 如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.
如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.